ГИПЕРГЕОМЕТРИЧЕСКАЯ ФУНКЦИЯ

ГИПЕРГЕОМЕТРИЧЕСКАЯ ФУНКЦИЯ - решение гипергеометрического уравнения

z(1 - z)w'' + [γ - (α + β + 1) z] w' - αβw = 0. (1)

Г. ф. может быть определена с помощью так наз. ряда Гаусса:

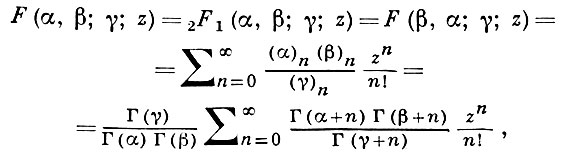
где α, β, γ - параметры, принимающие любые действительные или комплексные значения, кроме γ = 0, -1, -2, ..., z- комплексное переменное, (х)_n ≡ х(х + 1)...(х + n - 1). Функция F(α, β; γ; z) наз. гипергеометрической функцией 1-го рода. Второе линейно независимое решение гипергеометрич. уравнения (1)

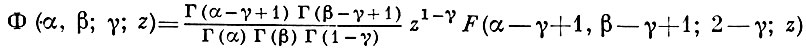
наз. гипергеометрической функцией 2-го рода.

Ряд (2) сходится абсолютно и равномерно при |z| < 1; сходимость распространяется и на единичную окружность, если Rе(α + β - γ) < 0; при 0 ≤ Rе(α + β - γ) < 1 сходится во всех точках единичной окружности, кроме z = 1. Однако существует аналитич. продолжение Г. ф. (2) во внешность единичной окружности |z| > 1 с разрезом (1, ∞) (см. [1]). Функция F(α, β; γ; z) - однозначная аналитическая в комплексной плоскости z с разрезом (1, ∞). Если α или β - нуль или целое отрицательное число, то ряд (2) обрывается на конечном числе членов и Г. ф. представляет собой полином относительно z.

При γ = -n, n = 0, 1, 2, ..., Г. ф. не определена, однако

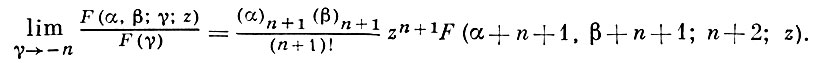
Элементарные соотношения. Шесть функций

F (α ± 1; β; γ; z), F(α, β ± 1; γ; z) F(α, β; γ ± 1; z)

наз. смежными с Г. ф. F(α, β; γ; z). Между функцией F(α, β; γ; z) и любыми двумя смежными с ней существует линейная зависимость. Напр.,

γF(α, β-1; γ; z) + (α - β)zF(α, β; γ + 1; z) = γF(α - 1, β; γ; z).

15 формул такого типа впервые были найдены К. Гауссом (С. Gauss, см. [2], [3]). Ассоциированные функции F(α + m, β + n; γ + l; z), где m, n, l -целые числа, могут быть получены повторными применениями соотношений Гаусса. Имеют место формулы дифференцирования

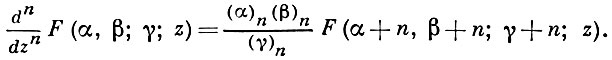
Уравнение (1) имеет 24 решения вида

z^ρ(1 - z)^σF(α', β'; γ'; z').

где ρ, σ, α', β' и γ' - линейные функции α, β и γ, z и z' связаны дробно-линейным преобразованием. Любые три решения линейно зависимы (см. [2]). Существуют квадратичные, кубичные и более высокого порядка преобразования (см. [2]-[5]).

Основные интегральные представления. Если Re γ > Rе β > 0 и |arg(1-z)| < π, то имеет место формула Эйлера:

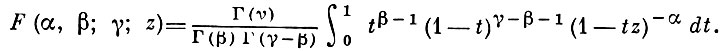
(3)

Разлагая (1 - tz)^-α в биномиальный ряд и применяя контурные интегралы для бета-функции, можно полунить другие интегральные представления (см. [2]). Интеграл (3) и другие аналогичные формулы, определяющие аналитич. функцию от z, однозначную во всей плоскости z, также могут служить для аналитич. продолжения функции F(α, β; γ; z) в область |arg(-z)| < π. Существуют и другие аналитич. продолжения (см. [1], [2]).

Асимптотическое поведение Г. ф. при больших значениях |z| полностью описывается с помощью формул, дающих аналитич. продолжение в окрестность точки z = ∞ (см. [1]-[3]). Если α, β, z - фиксированные числа и |γ| достаточно велико, |arg γ| < π - ε, ε > 0, то при |z| < 1:

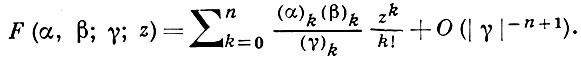
При |z| > 1 имеется аналогичное выражение.

Для фиксированных α, γ и z, γ ≠ 0, -1, -2, ...,

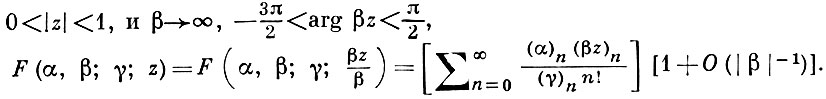
См. также [2], [5], [6].

Представления функции через Г. ф. Элементарные функции:

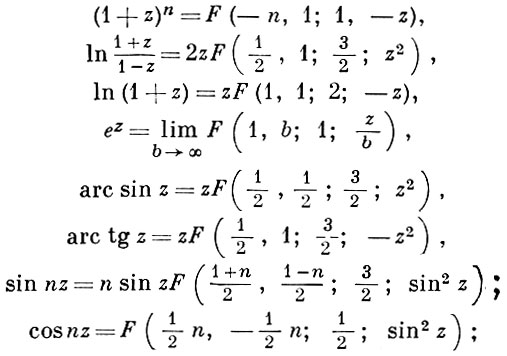
полные эллиптич. интегралы 1-го и 2-го рода:

K(z) = π/2 F(1/2; 1/2; 1; z²), E(z) = π/2 F(-1/2, 1/2; 1; z²);

присоединенные функции Лежандра:

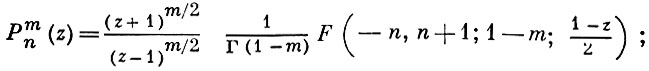
многочлены Чебышева:

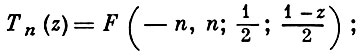
многочлены Лежандра:

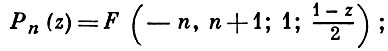
ультрасферические многочлены:

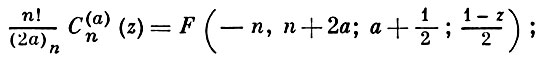
многочлены Якоби:

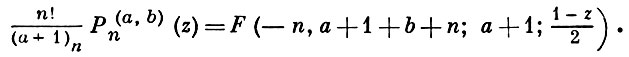
Обобщения Г. ф. Обобщенной Г. ф.

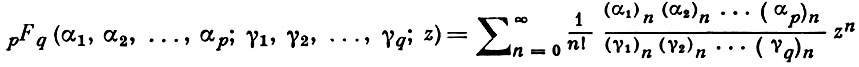
наз. решение гипергеометрич. уравнения (q+1)-го порядка (см. [2]). Имеются и другие обобщения Г. ф., напр., на случай многих переменных (см. [2]).

Лит.: [1] Лебедев Н. Н., Специальные функции и их приложения, 2 изд., М.-Л., 1963; [2] Бейтмен Г., Эрдейи А., Высшие трансцендентные функции, [т. 1], пер. с англ., 2 изд.,М., 1973; [3] Градштейн И. С., Рыжик И. М., Таблицы интегралов, сумм, рядов и произведений, 5 изд., М., 1971; [4] Кummеr Е. Е., «J. reine und angew. Math.», 1835, Bd 15, S. 39-83, 127-72; [5] Handbook of mathematical functions with formulas, graphs and mathematical tables, N. Y., 1964; [6] Уиттекер Э. Т., Ватсон Дж. Н., Курс современного анализа, ч. 2, Трансцендентные функции, пер. с англ., 2 изд., М., 1963; [7] Лебедев А. В., Федорова Р. М., Справочник по математическим таблицам, М., 1956; [8] Бурунова Н. М., Справочник по математическим таблицам, М., 1959, доп. 1; [9] An index of mathematical tables, 2 ed., v. 1,2, Oxford, 1962.

Э. А. Чистова.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.