ГИПЕРБОЛИЧЕСКОГО ТИПА УРАВНЕНИЕ

ГИПЕРБОЛИЧЕСКОГО ТИПА УРАВНЕНИЕ в данной точке М(x₁, ..., x_n) - дифференциальное уравнение с частными производными, для к-poro однозначно разрешима задача Коши при начальных данных, заданных в окрестности точки М на любой нехарактеристич. поверхности. В частности, дифференциальное уравнение с частными производными, для к-рого конус нормалей не имеет мнимых полостей, будет Г. т. у. Дифференциальное уравнение

L(u) = H(D₁, ..., D_n)u + F(D₁, ..., D_n)u + G(x) = 0, (*)

где D_i = ∂/∂x_i, i = 1, ..., n, H(D₁, ..., D_n) - однородный многочлен степени m, а многочлен F имеет степень, меньшую чем m, наз. Г. т. у., если его характеристич. уравнение

Q(ξ₁, ..., ξ_n) = H(ξ₁, ..., ξ_n) = 0

имеет n различных и действительных решений относительно одной из величин ξ₁, ..., ξ_n при заданных остальных. Любое уравнение (*) 1-го порядка (m = 1) с действительными коэффициентами есть Г. т. у. Для уравнений 2-го порядка

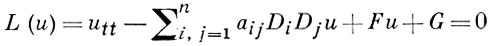
гиперболичность гарантируется положительной определенностью квадратичной формы

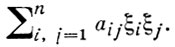
Б. Л. Рождественский.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.