ГИПЕРБОЛИЧЕСКИЙ ПАРАБОЛОИД

ГИПЕРБОЛИЧЕСКИЙ ПАРАБОЛОИД - незамкнутая нецентральная поверхность второго порядка. В надлежащей системе координат (см. рис.) уравнение Г. п. имеет вид:

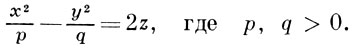
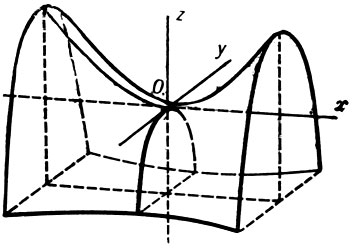
Сечения Г. п. плоскостями, параллельными плоскостям xOz и yOz, являются параболами, а сечения плоскостями, параллельными плоскости хОу,- гиперболами (плоскостью хОу - двумя прямыми). Ось симметрии Г. п. наз. его осью; точка пересечения Г. п. с осью наз. вершиной Г. п. Если p = q, то Г. п. имеет две оси симметрии. Г. п.- линейчатая поверхность;

уравнения прямолинейных образующих, проходящих через данную точку (х₀, у₀, z₀) Г. п., имеют вид:

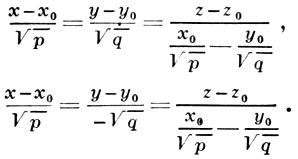
А. Б. Иванов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.