ГИПЕРБОЛИЧЕСКАЯ МЕТРИКА

ГИПЕРБОЛИЧЕСКАЯ МЕТРИКА, гиперболическая мера, - метрика в области комплексной плоскости, обладающей по крайней мере тремя граничными точками, инвариантная относительно автоморфизмов этой области.

Гиперболическая метрика в круге Е : |z| < 1 определяется линейным элементом

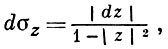
где |dz| - линейный элемент евклидовой длины. Введение Г. м. в круге Е приводит к модели Лобачевского, геометрии. Роль прямых в данной модели играют дуги евклидовых окружностей, ортогональных к |z| = 1, лежащие в Е; роль бесконечно удаленной точки играет окружность |z| = 1. Движениями в ней служат дробно-линейные преобразования круга Е на себя. Гиперболическая длина кривой L, лежащей в круге Е, определяется формулой

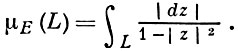
Гиперболическое расстояние между точками z₁ и z₂ круга Е равно

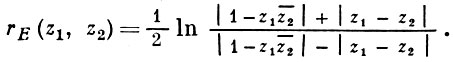
Множество точек круга Е, гиперболич. расстояние к-рых от данной точки z₀, z₀ ∈ E, не превосходит заданного числа R, R > 0, т. е. гиперболический круг в Е с гиперболич. центром в точке z₀ и гиперболич. радиусом R, является евклидовым кругом с центром, отличным от z₀ при z₀ ≠ 0.

Гиперболическая площадь области В, лежащей в Е, определяется формулой

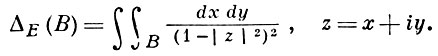
Величины μ_E(L), r_E(z₁, z₂) и Δ_E(B) инвариантны относительно дробно-линейных преобразований круга Е на себя.

Гиперболическая метрика в любой области D плоскости z, имеющей не менее трех граничных точек, определяется как перенесенная в D при конформном отображении ζ = ζ(z) области D на круг Е: |ζ| < 1 гиперболич. метрика круга Е: ее линейный элемент определяется формулой

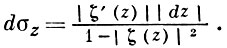
Область, имеющую не более двух граничных точек, уже нельзя конформно отобразить на круг. Величина

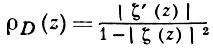
наз. плотностью Г. м. области D. Гиперболич. метрика области D не зависит ни от выбора отображающей функции, ни от выбора ее ветви и вполне определяется областью D и положением точек в D. Гиперболич. длина кривой L, лежащей в D, находится по формуле

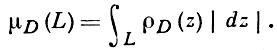
Гиперболическое расстояние между точками z₁ и z₂ области D равно

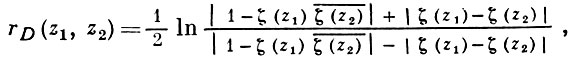
где ζ(z) - любая функция, конформно отображающая D на круг Е. Гиперболическим кругом в области D, как и в случае круга |z| < 1, наз. множество точек области D, гиперболич. расстояние к-рых от данной точки области D (гиперболич. центра) не превосходит заданного положительного числа (гиперболич. радиуса). Если область D многосвязна, гиперболич. круг в D есть, вообще говоря, многосвязная область. Гиперболическая площадь области В, лежащей в D, находится по формуле

Δ_D(B) = ∫∫_B ρ²_D(z) dx dy.

Величины μ_D(L), r_D(z₁, z₂) и Δ_D(B) являются инвариантами относительно конформных отображений области D (одно из основных свойств Г. м. в D).

Лит.: [1] Голузин Г. М., Геометрическая теория функций комплексного переменного, 2 изд., М., 1966; [2] Стоилов С., Теория функций комплексного переменного, пер. с рум., т. 1-2, М., 1962.

Г. В. Кузьмина.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.