ГИПЕРБОЛА

ГИПЕРБОЛА - плоская кривая, получающаяся в пересечении кругового конуса с плоскостью, не проходящей через вершину конуса и пересекающей обе его полости. Г. есть множество точек М плоскости

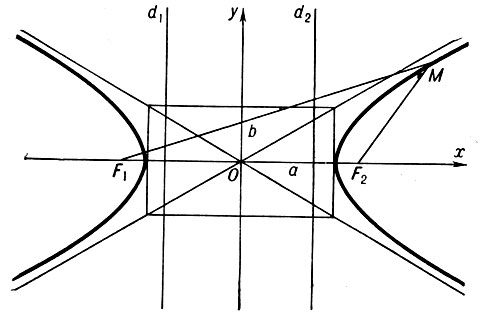
(см. рис.), модуль разности расстояний к-рых до двух данных точек F₁ и F₂ (фокусов Г.) постоянен и равен 2а < F₁F₂. Расстояние между фокусами Г. наз. фокусным расстоянием его принято обозначать через 2с. Середина отрезка F₁F₂ наз. центром Г. Прямая, на к-рой лежат фокусы Г., наз. действительной (или фокальной) осью Г. Прямая, проходящая через центр Г. перпендикулярно к действительной оси Г., наз. мнимой осью Г. Мнимая и действительная оси Г. являются ее осями симметрии. Число е = с/а < 1 наз. эксцентриситетом Г. Диаметром Г. наз. любая прямая, проходящая через центр Г. Середины параллельных хорд Г. лежат на диаметре. Директрисой Г., соответствующей данному фокусу F, наз. прямая d, перпендикулярная к действительной оси Г., отстоящая от центра на расстояние a/e и лежащая от центра по одну сторону с фокусом F. У Г.- две директрисы. Г. имеет две асимптоты:

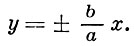
Г. есть центральная линия второго порядка. Ее канонич. уравнение имеет вид

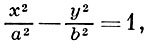
где a и

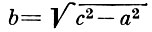
- полуоси Г., a х, у - текущие координаты. Уравнение касательной к Г. в точке (х₀, у₀) имеет вид

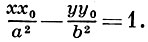
Фокальный параметр Г. (половина длины хорды, проходящей через фокус перпендикулярно фокальной оси Г.) равен b²/a. При помощи фокального параметра р можно записать уравнение Г. в виде

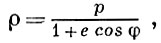
где ρ, φ - полярные координаты, π - φ₀ < φ < π + φ₀, 2φ₀ - угол между асимптотами.

При а = b Г. наз. равнобочной, или равносторонней, Г. Асимптоты равнобочной Г. взаимно перпендикулярны; если их принять за оси координат, то уравнение равнобочной Г. примет вид

y = k/x,

т. е. равнобочная Г. представляет собой график обратно Пропорциональной зависимости.

А. Б. Иванов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.