ГИЛЬБЕРТОВО ПРОСТРАНСТВО

ГИЛЬБЕРТОВО ПРОСТРАНСТВО - векторное пространство H над полем комплексных (или действительных) чисел вместе с комплексной (действительной) функцией (х, у), определенной на Н × Н и обладающей следующими свойствами.

1) (х, x) = 0 в том и только в том случае, если х = 0;

2) (х, х) ≥ 0 для всех х ∈ Н;

3) (х+у, z) = (x, z) + (y, z), х, у, z ∈ H;

4) (αх, у) = α(х, у), х, у ∈ H, α - комплексное (действительное) число;

5) (х, у) = ̅(у, х), х, у ∈ H;

6) если х_n ∈ Н, n = 1, 2, ... и если

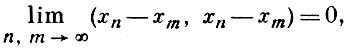
то существует такой элемент х ∈ Н, что

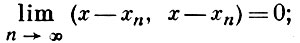
элемент х наз. пределом последовательности (х_n);

7) H - бесконечномерное векторное пространство.

Функция (х, у), удовлетворяющая аксиомам 1)-5), наз. скалярным произведением, или внутренним произведением, элементов х и у. Величина ||x|| = (х, х)^1/2 наз. нормой (или длиной) элемента х ∈ Н. Имеет место неравенство |(x, у)| ≤ ||х||⋅||у||. Если ввести в H расстояние между элементами х, y, ∈ H при помощи равенства ρ(х, у) = ||х - у||, то H превращается в метрическое пространство.

Два Г. п. H и Н₁ наз. изоморфными (или изометрически изоморфными), если существует взаимно однозначное соответствие х ↔ x₁, х ∈ Н, х₁ ∈ H₁, между H и H₁ сохраняющее линейные операции и скалярное произведение.

Г. п. составляют наиболее распространенный и важный для приложений класс бесконечномерных векторных пространств. Они представляют собой естественное обобщение понятия конечномерного векторного пространства со скалярным произведением (т. е. конечномерного евклидова пространства, или конечномерного унитарного пространства). Именно, если в конечномерном векторном пространстве (над полем действительных или комплексных чисел) задано скалярное произведение, то свойство 6), наз. полнотой Г. п., выполняется автоматически. Бесконечномерные векторные пространства H со скалярным произведением наз. предгильбертовыми пространствами; существуют предгильбертовы пространства, в к-рых свойство 6) не выполняется. Всякое предгильбертово пространство может быть дополнено до Г. п.

Иногда в определение Г. п. не включается условие бесконечномерности, т. е. предгильбертовым пространством наз. векторное пространство над полем комплексных (или действительных) чисел со скалярным произведением, а Г. п. наз. полное предгильбертово пространство.

Примеры Г. п. 1) Комплексное пространство l² (или l₂). Элементами этого Г. п. являются бесконечные последовательности комплексных чисел х = {ξ₁, ξ₂, ...}, y = {η₁, η₂, ...}, со сходящейся суммой квадратов модулей:

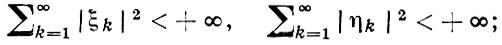
скалярное произведение определяется равенством

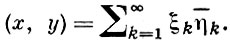
2) Пространство l²(Т) (обобщение примера 1)). Пусть Т - произвольное множество. Элементами Г. п. l²(Т) являются комплекснозначные функции х(t) на T, отличные от нуля не более чем в счетном множестве точек t ∈ Т и такие, что ряд

∑_t∈T |x(t)|²

сходится. Скалярное произведение определяется равенством

(x, y) = ∑_t∈T x(t) y̅(t).

Всякое Г. п. изоморфно пространству l²(Т) для нек-рого соответствующим образом подобранного Т.

3) Пространство L²(S, Σ, μ) (или L₂(s, Σ, μ)) комплекснозначных функций x(s), определенных на множестве S с вполне аддитивной положительной мерой μ (заданной на σ-алгебре Σ-подмножеств множества S) измеримых и имеющих интегрируемый квадрат модуля:

∫_S |x(s)|² dμ(s) < +∞.

В этом Г. п. скалярное произведение определяется равенством

(х(s), у(s)) = ∫_S x(s)y̅(s) dμ (s).

4) Соболева пространство W²_l(Ω), обозначаемое также Н_(l) (см. Вложения теоремы).

5) Г. п. функций со значениями в Г. n Пусть Н -нек-рое Г. п. со скалярным произведением (х, у), х, у ∈ Н. Пусть, далее, Ω - произвольная область в R_n, a f(x), х ∈ Ω - функция со значениями в H, измеримая в смысле Бохнера (см. Бохнера интеграл) и такая, что

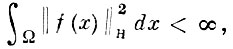
где dx - мера Лебега на Ω (вместо меры Лебега можно взять любую другую положительную счетно аддитивную меру). Если на этом множестве функций определить скалярное произведение

(f(x), g(x))_⊥ = ∫_Ω (f(x), g(x)) dx,

то получится новое Г. п. H₁.

6) Множество непрерывных Бора почти периодических функций на прямой образует предгильбертово пространство, если скалярное произведение определяется равенством

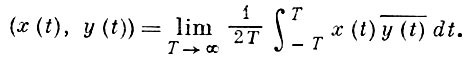
Существование предела вытекает из теории почти периодич. функций. Это пространство пополняется Безиковича почти периодическими функциями класса В².

Пространства l² и L² были введены и изучены Д. Гильбертом [1] в основополагающих работах по теории интегральных уравнений и бесконечных квадратичных форм. Определение Г. п. было дано Дж. Нейманом [3], Ф. Риссом [4] и М. Стоуном [13], к-рые положили также начало его систематич. изучению.

Г. п. является естественным обобщением обычного трехмерного пространства евклидовой геометрии, и многие геометрич. понятия имеют интерпретацию в Г. п., что позволяет говорить о геометрии Г. п. Два вектора x, y из Г. п. Н наз. ортогональными (x ⊥ f), если (x, у) = 0. Два линейных многообразия и из H наз. ортогональными (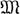 ⊥ 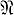), если каждый элемент из 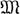ортогонален каждому элементу из 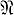. Ортогональным дополнением множества А ⊂ Н называется множество В = {х| (х, A) = 0}, т. е. множество элементов х ∈ Н, ортогональных ко всем элементам из А. Оно обозначается H ⊖ A или, если Н подразумевается, А^⊥. Ортогональное дополнение 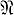произвольного множества 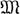из Н есть замкнутое линейное многообразие. Если 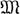-замкнутое линейное многообразие в Г. п. (называемое также подпространством), то всякий элемент х ∈ Н единственным образом может быть представлен в виде суммы х = у + z, у ∈ 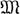, z ∈ 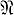. Это разложение наз. теоремой об ортогональном дополнении и записывается обычно в виде

H = ⊕ .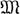

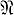При этом теорема справедлива также в случае, если Н есть предгильбертово пространство, а 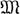- замкнутое линейное многообразие в H. В связи с этим уместно отметить, что нек-рые другие утверждения теории Г. п. справедливы полностью или частично и в предгильбертовых пространствах. Однако практически это обстоятельство не очень существенно, ибо встречающиеся в приложениях пространства либо полны, либо известно, как их пополнить.

Множество А ⊂ Н наз. ортонормированным множеством, или ортонормированной системой, если любые различные два вектора из А ортогональны и если норма каждого вектора у ∈ А равна единице. Ортонормированное множество наз. полным ортонормированным множеством, если не существует ненулевого вектора из H, ортогонального ко всем векторам этого множества. Если {у_i} - ортонормированная последовательность, а {α_i} - последовательность скаляров, то ряд

∑_i α_iy_i

сходится в том и только в том случае, когда

∑_i |α_i|² < ∞

при этом

||∑_i α_iy_i||² = ∑_i |α_i|²

(теорема Пифагора в Г. п.).

Пусть А - ортонормированное множество в Г. п. H, а х - произвольный вектор из H. Тогда (х, у) = 0 для всех у ∈ А, за исключением конечного или счетного множества векторов. Ряд

Рх = ∑_y∈A (x, y) y

сходится, и его сумма не зависит от порядка расположения его ненулевых членов. Оператор Р является оператором ортогонального проектирования, или проектором, на замкнутое линейное многообразие, порождаемое множеством А.

Множество А ⊂ Н наз. ортонормированным базисом линейного многообразия 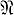⊆ H, если А содержится в 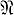и если для любого х ∈ 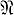имеет место

x = ∑_y∈A (x, y) y

т. е. любой вектор х ∈ 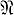разлагается по системе А, или может быть представлен при помощи векторов системы А. Набор чисел {(х, у)| у ∈ А} наз. набором коэффициентов Фурье элемента х по базису А. Каждое подпространство Г. п. H (в частности, само H) имеет ортонормированный базис.

В l²(Т) ортонормированным базисом является набор функций {x_t, t ∈ T}, определяемых формулой x_t(s) = 1 при s = t, x_t(s) = 0 при s ≠ t. В пространстве L²(s, Σ, μ) разложение вектора по базису принимает вид разложения функции по системе ортогональных функций -важный метод решения задач математич. физики.

Для ортонормированного множества A ⊂ H следующие утверждения эквивалентны: А полно; А является ортонормированным базисом для H; ||x||² = Σ_y∈A|(х, у)|² для любого х ∈ H.

Все ортонормированные базисы данного Г. п. имеют одну и ту же мощность. Этот факт позволяет определить размерность Г. п. Именно, размерностью Г. п. наз. мощность произвольного ортонормированного базиса в нем. Иногда эта размерность наз. гильбертовой размерностью (в отличие от линейной размерности Г. п., т. е. мощности базиса Гамеля (Хамеля) - понятия, не учитывающего топологич. структуру Г. п.). Два Г. п. изоморфны в том и только в том случае, когда они имеют одну и ту же размерность. С понятием размерности связано понятие дефекта, или коразмерности, подпространства. Именно, дефектом подпространства H₁ Г. п. H наз. размерность ортогонального дополнения H^⊥₁ = H ⊖ H₁. Подпространство, дефект к-рого равен 1, т. е. ортогональное дополнение к-рого одномерно, называется гиперпространством. Параллельное ему плоское множество называется гиперплоскостью.

Некоторые из геометрич. понятий требуют использования терминологии линейных операторов в Г. п.; к ним относится, в частности, понятие раствора линейных многообразий. Раствором многообразий М₁ и М₂ в Г. п. H наз. норма θ(М₁, М₂) разности операторов, проектирующих H на замыкание этих линейных многообразий.

Простейшие свойства раствора:

а) θ(М₁, М₂) = θ(М̅₁, M̅₂) = θ(H ⊖ M̅₁, H ⊖ M̅₂);

б) θ(М₁, М₂) ≤ 1,

причем в случае строгого неравенства dim M₁ = dim М₂.

Во многих задачах, относящихся к Г. п., участвуют лишь конечные наборы векторов Г. п., т. е. элементы конечных линейных многообразий Г. п. Поэтому понятия и методы линейной алгебры играют в теории Г. п. большую роль. Векторы g₁, g₂, ..., g_n в Г. п. наз. линейно независимыми, если равенство

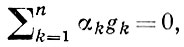
где α_k - скаляры, возможно лишь в том случае, когда все α_k равны нулю. Для линейной независимости векторов необходимо и достаточно, чтобы их Грама определитель был отличен от нуля. Счетная последовательность векторов g₁, ..., g_n, ... наз. линейно независимой последовательностью, если линейно независима каждая ее конечная часть. Каждая линейно независимая последовательность может быть ортогонализирована, т. е. может быть построена такая ортонормированная система е₁, е₂, ..., что для каждого n линейные оболочки множеств {g_k}ⁿ_k=1 и {e_k}ⁿ_k=1 совпадают. Это построение наз. процессом ортогонализации (ортонормализации) Грама-Шмидта и осуществляется следующим образом:

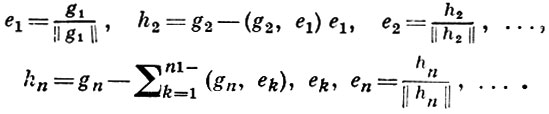
В множестве Г. п. определены операции прямой суммы и тензорного произведения Г. п. прямой суммой Г. п. H_i, i = 1, 2, ..., n, где каждое H_i обладает соответствующим скалярным произведением, наз. Г. п.

Н = Н₁ ⊕ Н₂ ⊕ ... ⊕ Н_n,

определяемое следующим образом: в векторном пространстве Н₁ +̇ Н₂ +̇ ... +̇ Н_n - прямой сумме векторных пространств H₁, ..., H_n - задается скалярное произведение равенством

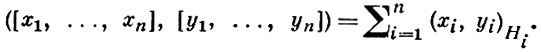
При i ≠ j элементы из H_i и H_j в прямой сумме

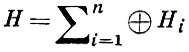
взаимно ортогональны, и проектирование H на H_i совпадает с ортогональным проектированием H на H_i. Понятие прямой суммы Г. п. обобщается на случай бесконечного множества прямых слагаемых. Пусть для каждого ν из нек-рого множества А индексов задано Г. п. H_ν. Прямой суммой Г. п. наз. (и обозначается Σ_ν∈A ⊕ H_ν) совокупность H всех определенных на А функций {x_ν}, обладающих тем свойством, что x_ν ∈ H_ν для каждого ν ∈ A, и ∑_ν∈A ||x_ν||² < ∞. При этом в H линейные операции определяются равенством

{x_ν} + {y_ν} = {x_ν + y_ν}, α{x_ν} = {αx_ν},

и скалярное произведение - равенством

({x_ν}, {y_ν}) = ∑_ν∈A (x_ν, y_ν) _Hν.

При таком способе введения линейных операций и скалярного произведения прямая сумма

H = ∑_ν∈A ⊕ H_ν

становится Г. п.

Другой важной операцией в множестве Г. п. является тензорное произведение. Тензорным произведением Г. п. H_i, i = 1, 2, ..., n, наз. Г. п., определяемое следующим образом. Пусть H₁ ⊙ H₂ ⊙ ... ⊙ H_n - тензорное произведение векторных пространств H₁, ..., H_n. В векторном пространстве H₁ ⊙ H₂ ⊙ ... ⊙ H_n существует единственное скалярное произведение такое, что

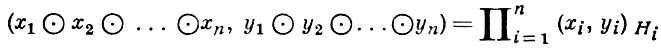
для всех х_i, у_i ∈ H_i. Векторное пространство становится, таким образом, предгильбертовым пространством, пополнение к-рого есть Г. п., обозначаемое H₁ ⊕ H₂ ⊕ ... ⊕ H_n или 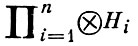и наз. тензорным произведением Г. п. H_i.

Г. п. образуют важный класс банаховых пространств: любое Г. п. H есть банахово пространство относительно нормы ||x|| = (x, х)^1/2, причем для любых двух векторов х, у ∈ Н имеет место равенство параллелограмма:

||x + у||² + ||x - y||² = 2(||x||² + ||y||²).

Равенство параллелограмма выделяет класс Г. п. среди банаховых пространств, т. е. если в действительном нормированном пространстве В для любой пары элементов х, у ∈ В имеет место равенство параллелограмма, то функция

(x, y) = 1/4(||x + y||² - ||x - y||²)

удовлетворяет аксиомам скалярного произведения и тем самым превращает В в предгильбертово пространство (а если В - банахово, то - в Г. п.). Из равенства параллелограмма следует, что Г. п. есть равномерно выпуклое пространство. Как в любом банаховом пространстве, в Г. п. можно определить две топологии -сильную (нормированную) и слабую. Эти топологии различны, но Г. п. сепарабельно в сильной топологии тогда и только тогда, когда оно сепарабельно в слабой топологии; выпуклое множество (в частности, линейное многообразие) в Г. п. сильно замкнуто тогда и только тогда, когда оно слабо замкнуто.

Как и в теории общих банаховых пространств, в теории Г. п. важную роль играет понятие сепарабельности. Г. п. сепарабельно тогда и только тогда, когда оно имеет счетную размерность. Г. п. l² и Н_(l) сепарабельны. Г. п. l²(Т) сепарабельно тогда и только тогда, когда Т не более чем счетно; Г. п. L²(s, Σ, μ) сепарабельно, если мера μ имеет счетный базис. Г. п. В² не сепарабельно.

Любой ортонормированный базис в сепарабельном Г. п. Н является одновременно безусловным базисом Шаудера в H, рассматриваемом как банахово пространство. Однако в сепарабельных Г. п. существуют и не ортогональные базисы Шаудера. Так, справедлива теорема (см. [7]): пусть {f_k} - полная система векторов в Г. п. H и пусть λ_n и Λ_n - наименьшее и наибольшее собственные значения Грама матрицы

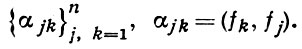
Если

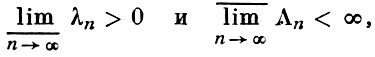
то 1) последовательность {f_k} есть базис в H; 2) существует биортогональная к {f_k} последовательность {g_k}, к-рая также является базисом в H.

Как и в любом банаховом пространстве, описание множества линейных функционалов на Г. п. и исследование свойств этих функционалов имеет большое значение. Линейные функционалы в Г. п. устроены особенно просто. Всякий линейный функционал f в Г. п. H однозначно записывается в виде f(x) = (x, х*) для всех х ∈ Н, где х* ∈ Н; при этом ||f||= ||х*||. Пространство H* линейных функционалов f на H, сопряженное к H, изометрически антиизоморфно H (т. е. соответствие f → x* изометрично, аддитивно и антиоднородно: αf → ᾱх*). В частности, Г. п. рефлексивно; поэтому справедливы следующие утверждения: Г. п. слабо секвенциально полно; для того чтобы подмножество Г. п. было относительно слабо компактным, необходимо и достаточно, чтобы оно было ограниченным.

Основным содержанием теории Г. п. является теория линейных операторов в Г. п. Само понятие Г. п. сформировалось в работах Д. Гильберта [2] и Э. Шмидта [14] по теории интегральных уравнений, а абстрактное определение Г. п. было дано в работах Дж. Неймана [3], Ф. Рисса [4] и М. Стоуна [13] по теории эрмитовых операторов. Теория операторов в Г. п. представляет особый важный раздел общей теории операторов по двум причинам.

Во-первых, теория самосопряженных и унитарных операторов в Г. п. является не только самой разработанной частью общей теории линейных операторов, но и имеющей исключительно широкие приложения в других областях функционального анализа и в ряде других разделов математики и физики. Теория линейных операторов в Г. п. позволяет рассмотреть многие задачи математич. физики с единой общей точки зрения; прежде всего - вопросы, относящиеся к собственным значениям и собственным функциям. Кроме того, теория самосопряженных операторов в Г. п. служит математич. аппаратом квантовой механики: при описании квантовомеханич. системы наблюдаемые (энергия, импульс, координаты и т. п.) интерпретируются как самосопряженные операторы в нек-ром Г. п., а состояние системы задается элементом этого Г. п. В свою очередь, задачи квантовой механики до настоящего времени оказывают влияние на развитие теории самосопряженных операторов, а также теории алгебр операторов в Г. п.

Во-вторых, интенсивно развивающаяся теория несамосопряженных операторов в Г. п. (в частности, циклических, нильпотентных, одноклеточных, сжимающих, спектральных и скалярных операторов) является важной моделью теории линейных операторов в более общих пространствах.

Важный класс линейных операторов в Г. п. образуют всюду определенные непрерывные операторы, наз. также ограниченными операторами в Г. п. Если ввести в множестве ℬ(H) всех ограниченных линейных операторов в H операции сложения, умножения на число и умножения операторов, а также норму оператора, по обычным правилам (см. Линейные операторы) и определить инволюцию в ℬ(H) как переход к сопряженному оператору, то ℬ(H) становится банаховой алгеброй с инволюцией. Важнейшими классами ограниченных операторов в Г. п. являются самосопряженные операторы, унитарные операторы и нормальные операторы, так как они обладают специальными свойствами по отношению к скалярному произведению. Эти классы операторов хорошо изучены; основным инструментом в их изучении являются простейшие из ограниченных самосопряженных операторов, а именно: операторы ортогонального проектирования, или ортогональные проекторы, часто называемые просто проекторами. Способ, позволяющий строить любые ограниченные самосопряженные, унитарные и нормальные операторы в комплексном Г. п. с помощью проекторов, дается спектральным разложением соответствующих операторов, особенно простым в случае сепарабельного Г. п.

Более сложным разделом теории линейных операторов в Г. п. является теория неограниченных операторов. Важнейшими неограниченными операторами в Г. п. являются замкнутые линейные операторы с плотной областью определения; в частности, неограниченные самосопряженные и нормальные операторы. Между самосопряженными и унитарными операторами в Г. п. существует взаимно однозначное соответствие, определяемое Кэли преобразованием. Большое значение имеет (в частности, в теории линейных дифференциальных операторов) класс симметричных операторов в Г. п. и теория самосопряженных расширений симметричных операторов.

Неограниченные самосопряженные и нормальные операторы в комплексном Г. п. H также допускают спектральное разложение. Спектральное разложение является большим достижением теории самосопряженных и нормальных операторов в Г. п. Оно соответствует классич. теории приведения эрмитовых и нормальных комплексных матриц в n-мерном унитарном пространстве. Именно спектральное разложение и связанное с ним операторное исчисление для самосопряженных и нормальных операторов обеспечивают теории операторов в Г. п. широкую область применения во многих разделах математики.

Для ограниченных самосопряженных операторов в l₂ спектральное разложение было найдено Д. Гильбертом [1], к-рый также ввел важное понятие разложения единицы для самосопряженного оператора. В современный период известно несколько подходов к спектральной теории самосопряженных и нормальных операторов. Один из наиболее глубоких дает теория банаховых алгебр. Спектральное разложение для неограниченного самосопряженного оператора было найдено Дж. Нейманом [3]. Его работе предшествовали важные исследования Т. Карлемана [8], к-рый получил спектральное разложение для случая симметрического интегрального оператора, а также впервые обнаружил, что между симметрическими ограниченными и неограниченными операторами полной аналогии нет. На важность понятия самосопряженного оператора впервые обратил внимание Э. Шмидт (см. [3], с. 62).

Следует отметить, что как для исследований Д. Гильберта, так и для более поздних исследований большое значение имели работы П. Л. Чебышева, А. А. Маркова, Т. И. Стилтьеса по классической моментов проблеме, Якоби матрицам и непрерывным дробям (см. [9]).

Лит.: [1] Нilbеrt D., Grundzüge einer allgemeinen Theorie der linearen Integralgleichungen, Lpz.-В., 1912; N. Y., 1953; [2] Вesiсоvitсh A. S., Almost periodic functions, Camb., 1932; [3] vоn Neumann J., «Math. Ann.», 1929, Bd 102, S. 49-131; [4] Riesz F., «Acta Sci. Math. Szeged», 1930, v. 5, № 1, p. 23-54; [5] Дьедонне Ж., Основы современного анализа, пер. с англ., М., 1964; [6] Бурбаки Н., Топологические векторные пространства, пер. с франц., М., 1959; [7] Ахиезер Н. И., Глазман И. М., Теория линейных операторов в гильбертовом пространстве, 2 изд., М., 1966; [8] Саrlеmаn Т., Sur les équations intégrates singulieres a noyau réel et symétrique, Uppsala, 1923; [9] Axиeзep H. И., Классическая проблема моментов и некоторые вопросы анализа, связанные с нею, М., 1961; [10] Данфорд Н., Шварц Дж., Линейные операторы, пер. с англ., М., 1962; [11] Рисе Ф., Секефальви-Надь Б., Лекции по функциональному анализу, пер. с франц., М., 1954; [12] Наймарк М. А., Линейные дифференциальные операторы, 2 изд., М., 1969; [13] Stone М., Linear transformation in Hilbert space and their applications to analisis, N. Y., 1932; [14] Колмогоров A. H., Фомин С. В., Элементы теории функций и функционального анализа, 3 изд., М., 1972.

Б. М. Левитан.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.