ГИЛЬБЕРТА-ШМИДТА ОПЕРАТОР

ГИЛЬБЕРТА-ШМИДТА ОПЕРАТОР - оператор А, действующий в гильбертовом пространстве Н такой, что для любого ортонормированного базиса {х_i} в Н выполнено условие:

||A||² = ∑_i ||Ax_i||² < ∞

(достаточно, однако, справедливости этого для нек-рого базиса). Г.-Ш. о. является компактным оператором, для s-чисел к-рого s_i(А) и для собственных чисел λ_i(А) имеет место:

∑_i|λ_i(А)|² ≤ ∑_i s²_i(А) = ||A||² = tr (А*А);

при этом А*А оказывается ядерным оператором (здесь А* - оператор, сопряженный к А, а tr С - след оператора С). Совокупность всех Г.-Ш. о. пространства А образует гильбертово пространство со скалярным произведением

〈А, B〉 = tr(AB*).

Если R_λ(А) = (А -λЕ)^-1 - резольвента А, а

det₂(Е - zA) = ∏_i (1 - zλ_i(А))е^zλ_i(A)

- его регуляризованный характеристический определитель, то выполнено неравенство Карлемана

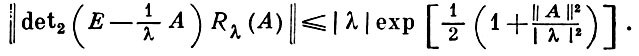
Типичный представитель Г.-Ш. о. - Гильберта-Шмидта интегральный оператор (откуда и название).

М. И. Войцеховский.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.