ГИЛЬБЕРТА СИНГУЛЯРНЫЙ ИНТЕГРАЛ

ГИЛЬБЕРТА СИНГУЛЯРНЫЙ ИНТЕГРАЛ - несобственный (в смысле главного значения по Коши) интеграл

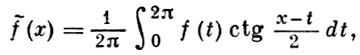
где периодич. функция f(t) наз. плотностью Г. с. и., a ctg((x-t)/2) - ядром Г. с. и. Если f(t) суммируема, то f̃(x) существует почти всюду, а если f(t) удовлетворяет условию Липшица с показателем α, 0 < α < 1, то f̃(x) существует при любом s и удовлетворяет тому же условию. Если f(x) суммируема с р-й степенью, р > 1, то f̃(х) обладает тем же свойством и

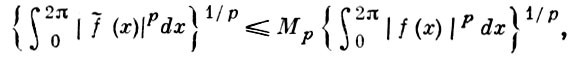
где М_p - постоянная, не зависящая от f(x). Кроме того, имеет место формула обращения Г. с. и.

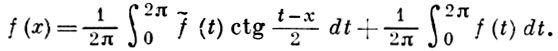
Функция f̃(x) наз. сопряженной с f(x).

Лит.: [1] Нilbеrt D., Grundzüge einer allgemeinen Theorie der linearen Integralgleichungen, Lpz.- В., 1912; [2] Riesz M., «Math. Z.», 1927, Bd 27, № 2, S. 218-44; [3] Бapи H. K., Тригонометрические ряды, M., 1961; [4] Mусxeлишвили Н. И., Сингулярные интегральные уравнения, 3 изд., М., 1968.

Б. В. Хведелидзе.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.