ГИЛЬБЕРТА ПРЕОБРАЗОВАНИЕ

ГИЛЬБЕРТА ПРЕОБРАЗОВАНИЕ функции f - несобственный интеграл

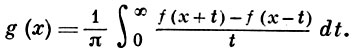
Если f ∈ L(-∞, ∞), то функция g существует пояти для всех значений х. Если f ∈ L_p(-∞, ∞), р ∈ (1, ∞), тогда функция g также принадлежит L_p(-∞, ∞) и почти всюду имеет место двойственная формула [обращение преобразования (1)]:

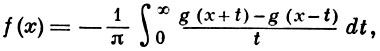
(2)

причем

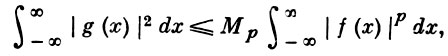
(3)

где константа М_p зависит только от р.

Формулы (1), (2) эквивалентны формулам

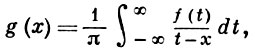
(4)

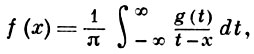
(5)

в к-рых интегралы понимаются в смысле главного значения.

Г. п. функции f называется также рассмотренный в смысле главного значения интеграл

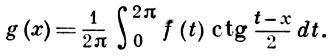
(6)

Этот интеграл часто наз. Гильберта сингулярным интегралом. В теории рядов Фурье функцию g, определяемую формулой (6), наз. сопряженной с f.

Если f ∈ L(0, 2π), то g существует почти всюду, а если f удовлетворяет условию Липшица с показателем α ∈ (0, 1), то g существует при любом x и удовлетворяет тому же условию. Если f ∈ L_p(0, 2π), р ∈ (1, ∞), то g обладает тем же свойством и имеет место неравенство, аналогичное (3), в к-ром интегралы взяты на интервале (0, 2π). Таким образом, интегральные операторы, порождаемые Г. п., являются ограниченными (линейными) операторами в соответствующих пространствах L_p.

Когда f удовлетворяет условию Липшица или f ∈ L_p(0, 2π) и, кроме того,

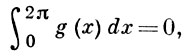
то имеет место двойственная формула

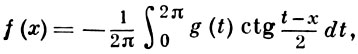
(7)

причем

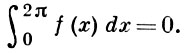
В классе функций, удовлетворяющих условию Липшица, равенство (7) справедливо всюду, а в классе функций, суммируемых с р-й степенью,- почти всюду.

Каждую из выписанных выше двойственных формул [напр. (4), (5)] можно рассматривать как интегральное уравнение 1-го рода; тогда вторая формула даст решение этого уравнения.

Когда функции ctg((t-x)/2) и 1/(t-x) рассматриваются как ядра интегральных операторов, то их часто наз. Гильберта ядром и Коши ядром. Между этими ядрами в случае единичной окружности существует простая связь:

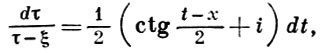
где ξ = e^ix, τ = е^it.

Лит.: [1] Нilbеrt D., Grundzüge einer allgemeinen Theorie der linearen Integralgleichungen, Lpz.-В., 1912 (2 Aufl., 1924); [2] Riesz M., «Math. Z.», 1927, Bd 27, № 2, S. 218-44; [3] Титчмарш E., Введение в теорию интегралов Фурье, пер. с англ., М.-Л., 1948; [4] Мусхелишвили Н. И., Сингулярные интегральные уравнения, 3 изд., М., 1968; [5] Бари Н. К., Тригонометрические ряды, М., 1961.

Б. В. Хведелидзе.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.