ГИЛЬБЕРТА НЕРАВЕНСТВО

ГИЛЬБЕРТА НЕРАВЕНСТВО - теорема Гильберта о двойных рядах:

(*)

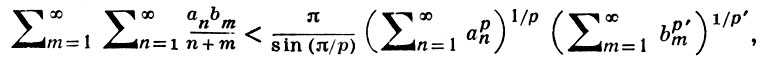
где

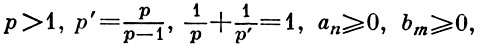
и ряды в правой части имеют конечные положительные суммы, причем константа π/sin(π/p) - точная, т. е. не может быть уменьшена. Д. Гильберт (D. Hilbert) доказал (*) без точной константы в своих лекциях по интегральным уравнениям. Его доказательство было опубликовано Г. Вейлем [1]. Точная константа найдена И. Шуром [2], а неравенство (*) с произвольным р > 1 впервые приводится в работах Г. Харди (G. Hardy) и М. Рисса (М. Riesz) в 1925. Имеются интегральные аналоги и обобщения неравенства (*), напр., неравенство

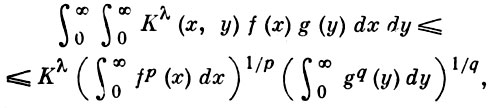
где К(х, у) - неотрицательное ядро, однородное со степенью -1, р > 1, q > 1, λ = 1/р + 1/q ≤ 1, f(х) ≤ 0, g(y) ≥ 0 и

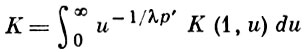
и полученный ранее [4] частный случай этого неравенства с ядром К(х, у) = 1/(х + у) (так наз. двупараметрическое Г. н.) и константой K^λ = (π/sin λр')^λ. Точность этой константы доказана при q' = p. Она является также асимптотически точной при р → 1 и произвольном допустимом фиксированном q. Вопрос об асимптотике константы в (*) для конечных сумм (1 ≤ n, m ≤ N) не решен (1977); здесь известно только, что при p = q = 2 константа равна

Лит.: [1] Weyl Н., Singuläre Integralgleichungen mit besonderer Berücksichtigung des Fourielschen Integraltheorems, Inaugural Dissertation, Gött., 1908; [2] Schur I., «J. für Math.», Bd 140, 1911, S. 1-28; [3] Xapди Г. Г., Литтльвуд Д. Е., Полиа Г., Неравенства, пер. с англ., М., 1948; [4] Воnsаll F. F., «Quart. J. Math.», 1951, v. 2, p. 135-50; [5] Levin V., «J. London Math. Soc.», 1936, v. 11, p. 119-24; [6] De Bruijn N. G., Wilf H. S., «Bull. Amer. Math. Soc.», 1962, v. 68, p. 70-3; [7] Walker P. L., «Рrос. Edinburgh Math. Soc.», 1973, v. 18, № 4, p. 293-94.

E. К. Годунова.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.