ГИЛЬБЕРТА МНОГОЧЛЕН

ГИЛЬБЕРТА МНОГОЧЛЕН градуированного модуля

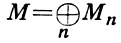
- многочлен, выражающий при больших натуральных n размерности однородных слагаемых модуля как функцию от n. Более точно, справедлива теорема, доказанная по существу Д. Гильбертом. Пусть A = K[X₀, ..., Х_m] - кольцо многочленов над полем K, градуированное так, что X_i являются однородными элементами степени 1, и пусть 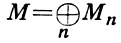- градуированный А-модуль конечного типа; тогда существует такой многочлен P_M(t) с рациональными коэффициентами, что для достаточно больших n dim_KM_n = Р_M(n). Этот многочлен наз. многочленом Гильберта.

Наибольший интерес представляет интерпретация Г. м. градуированного кольца R, являющегося фактор-кольцом кольца А по однородному идеалу I; в этом случае Г. м. доставляет проективные инварианты проективного многообразия X = Proj(R) ⊂ Р^m, определяемого идеалом I. В частности, степень многочлена P_R(t) совпадает с размерностью многообразия X, а р_a(X) = (-1)^{dim X}(Р_R(0) - 1) наз. арифметическим родом многообразия X. Через Г. м. выражается также степень вложения Х ⊂ Р^m. Г. м. кольца R называют также Г. м. проективного многообразия X относительно вложения X ⊂ P^m. Если O_X(1) - обратимый пучок, соответствующий этому вложению, то

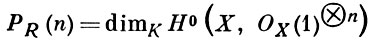
для достаточно больших n.

Лит.: [1] Hilbert D., Gesammelte Abhandlungen, Bd 2, В., 1933; [2] Бальдассарри М., Алгебраические многообразия, пер. с англ., М., 1961; [3] Зарисский О., Самюэль П., Коммутативная алгебра, т. 2, пер. с англ., М., 1963.

В. И. Данилов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.