ГИББСА ЯВЛЕНИЕ

ГИББСА ЯВЛЕНИЕ - особенность поведения частных сумм (или их средних) рядов Фурье. Впервые обнаружена Г. Уилбрейамом [1] и значительно позже переоткрыта Дж. Гиббсом [2]. Пусть частные суммы s_n(x) ряда Фурье функции f(x) сходятся к f(x) в нек-рой окрестности {х : 0 <|x - x₀| < h} точки х₀, в к-рой

a ≡ f(x₀ - 0) ≤ f(x₀ + 0) ≡ b.

В точке х₀ имеет место Г. я. для s_n(x), если А < а ≤ b < В, где

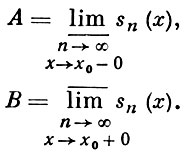
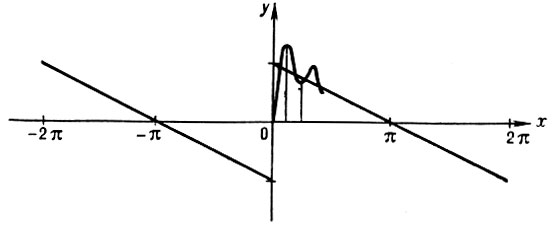
Геометрически это означает, что графики (рис.) частных сумм s_n(х) при х → х₀ и n → ∞ приближаются не к «ожидаемому» отрезку [a, b] по оси ординат, а к строго большему отрезку [А, В]. Аналогично определяется Г. я. для средних от частных сумм ряда Фурье при суммировании его тем или иным методом.

Для 2π-периодич. функций f с ограниченным изменением на [-π, π] справедливы, напр., утверждения (см. [3]).

1) В точках неустранимого разрыва (и только в них) имеет место Г. я. для s_n(x). В частности, если f(х) = (π - х)/2 при 0 < x < 2π, то для точки х₀ отрезок [а, b] = [-π/2, π/2], а отрезок [А, В]=[-l, l], где

2) Существует такая абсолютная постоянная α₀, 0 < α₀ < 1, что средние Чезаро σ^α_n(х) при α ≥ α₀ не имеют Г. я., а при α < α₀ оно наблюдается в каждой точке неустранимого разрыва функции f.

Лит.: [1] Willbraham Н., «Cambridge and Dublin Math. J.», 1848, v. 3, p. 198-201; [2] Gibbs J. W., «Nature», 1898, v. 59, p. 200; [3] Зигмунд А., Тригонометрические ряды, пер. с англ., т. 1, 2, М., 1965.

П. Л. Ульянов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.