ГЕТЕРОКЛИНИЧЕСКАЯ ТОЧКА

ГЕТЕРОКЛИНИЧЕСКАЯ ТОЧКА - такая точка (р = р*, q = q*), принадлежащая области определения функции Гамильтона H = Н(р, q) гамильтоновой системы

(*)

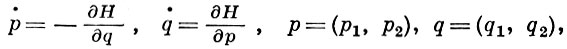
что решение системы (*), проходящее через эту точку, при t → ∞ асимптотически приближается к нек-рому периодич. решению Т₁, а при t → -∞ асимптотически приближается к другому периодич. решению Т'₁. При этом само решение, проходящее через Г. т., наз. гетероклиническим.

Существует связь между гетероклинич. решениями системы (*) и двумерными инвариантными поверхностями этой системы. Если двумерная инвариантная поверхность разделяет периодич. решения Т₁ и Т'₁, то не существует гетероклинич. решения, соединяющего эти периодич. решения. Во многих случаях справедливо и обратное. В невырожденном случае в окрестности гомоклинич. решения (см. Гомоклиническая точка) существует бесконечная последовательность периодич. решений, из к-рых любые два можно соединить гетероклинич. решением. Окрестность контура, составленного из конечного числа периодических и гетероклинических решений системы (*) (так наз. гомоклинического контура), обладает структурой, во многом сходной со структурой гомоклинич. решения.

Сформулированное выше определение Г. т. почти дословно переносится на случай гамильтоновой системы с числом степеней свободы n > 2, если периодич. решения Т₁ и Т'₁ заменить инвариантными торами T_k и T'_k размерности k и k' соответственно, 0 < k, k' < n. Гетероклинич. решения играют важную роль в изучении неустойчивости в гамильтоновых системах с числом степеней свободы больше двух и в теории грубых динамич. систем (см. Грубая система).

Лит.: [1] Пуанкаре А., Новые методы небесной механики, гл. 33, Избр. тр., пер. сфранц., т. 2, М., 1972; [2] Zehnder Е., «Gommuns Pure and Appl. Math.», 1973, v. 26, № 2, p. 131-82; [3] Мельникове. К., «Тр. Моск. матем. об-ва», 1963, т. 12, с. 3-52; [4] Смейл С., «Математика», 1967, т. 11, № 4, с. 69-78, 88-106; [5] Шильников Л. П., «Матем. сб.», 1967, т. 74(116), № 3, с. 378-97; [6] Алексеев В. М., «Матем. сб.», 1968, т. 76(118), № 1, с. 72-134; т. 77 (119) № 4, с. 545-601; 1969, т. 78 (120), № 1, с. 3-50.

В. К. Мельников.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.