ГЕРГЛОТЦА ФОРМУЛА

ГЕРГЛОТЦА ФОРМУЛА - интегральное соотношение, устанавливающее связь между двумя замкнутыми изометричными ориентируемыми регулярными поверхностями. Пусть на поверхностях S₁ и S₂ введены локальные координаты u и v так, что по их равенству устанавливается отображение изометрии. Пусть:

ds² = Edu² + 2Fdudv + Gdv²

- общая для S_α, α = 1, 2, первая квадратичная форма, К - гауссова кривизна, Н_α - средние кривизны и

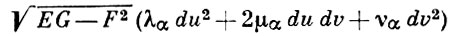
- вторые квадратичные формы поверхностей S_α. Тогда Г. ф. имеет вид:

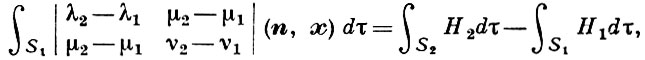
где x = x(u, v) - радиус-вектор поверхности S₁, n -единичный вектор нормали к S₁, dτ - элемент площади. Получена Г. Герглотцем [1].

Лит.: [1] Herglotz G., «Abh. math. Semin. Univ. Hamburg», 1943, Bd 15, S. 127-29; [2] Ефимов H. В., «Успехи матем. наук», 1948, т. 3, в. 2(24), с. 47-158.

Е. В. Шикин.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.