ГЕОМЕТРИЯ ЧИСЕЛ

ГЕОМЕТРИЯ ЧИСЕЛ, геометрическая теория чисел,- раздел теории чисел, изучающий теоретико-числовые проблемы с применением геометрич. методов. Г. ч. в собственном смысле сформировалась с выходом основополагающей монографии Г. Минковского [1] в 1896. Исходным пунктом направления, развившегося в самостоятельный раздел теории чисел, явилось то обстоятельство (подмеченное Г. Минковским), что нек-рые предложения, почти очевидные при рассмотрении фигур в n-мерном евклидовом пространстве, имеют глубокие следствия в теории чисел.

Основной и типичной задачей Г. ч. является задача об арифметич. минимуме m(F) нек-рой действительной функции

F(x) = F(x₁, ..., x_n);

при этом под m(F) понимается точная нижняя граница значений функции F(x), когда х пробегает все целые точки (т. е. точки с целочисленными координатами), удовлетворяющие нек-рому дополнительному условию (напр., условию х ≠ 0). В важнейших частных случаях эта задача решается теоремой Минковского о выпуклом теле, к-рая может быть сформулирована так: пусть F(x) < 1 есть n-мерное выпуклое тело объема V_F, причем F(-x) = F(x); тогда

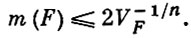
Значение m(F) позволяет судить об условиях существования решений диофантова неравенства (см. Диофантовы приближения)

|F(x)| ≤ c;

к этому вопросу сводятся многие задачи теории чисел. Особым разделом Г. ч. является геометрия квадратичных форм.

В Г. ч. различают два общих типа проблем, наз. однородной и неоднородной проблемами.

Однородная проблема, исследования по к-рой составляют большую часть Г. ч., посвящена изучению однородных минимумов m(F, Λ) лучевой функции F в точечной решетке Λ. Понятие точечной решетки является основным понятием Г. ч. Пусть a₁, ..., a_n -линейно независимые векторы n-мерного евклидова пространства. Множество точек

{g₁a₁ + ... + g_na_n},

когда g₁, ..., g_n пробегают независимо друг от друга все целые числа, наз. (точечной) решеткой Λ с базисом а₁, ..., а_n и определителем

d(Λ) = |det (а₁, ..., а_n)|.

Пусть в ℝⁿ заданы лучевая функция F = F(x) и решетка Λ определителя d(Λ). Точная нижняя граница

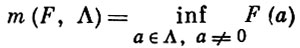
значений функции F в точках а ≠ 0 решетки Λ наз. минимумом функции F в решетке Λ (точнее, однородным арифметическим минимумом). Точная нижняя граница m(F, Λ), к-рая может и не достигаться, заведомо достигается для ограниченного звездного тела, определяемого неравенством

F(x) < 1.

Для оценки m(F, Λ) сверху важно уметь вычислять или оценивать постоянную Эрмита γ(F) лучевой функции F, определяемую равенством

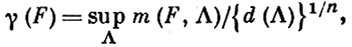
где точная верхняя граница берется по множеству ℤ_n всех n-мерных решеток Λ.

Центральным пунктом Г. ч. является установление связи между γ(F), критич. определителем (см. ниже) Δ(_F) множества _F = {x | F(x) < 1} и (если F - симметричная выпуклая лучевая функция) плотностью θ(_F) плотнейшей решетчатой упаковки тела _F.

Пусть в n-мерном евклидовом пространстве ℝⁿ заданы множество и решетка Λ определителя d(Λ). Решетка А наз. допустимой для или -допустимой, если не содержит точек из Λ, отличных от 0. Множество , имеющее хотя бы одну допустимую решетку, наз. множеством конечного типа; в противном случае наз. множеством бесконечного типа. Пусть -множество конечного типа; точная нижняя граница

Δ() = inf d(Λ)

множества определителей d(Λ) всех -допустимых решеток Λ наз. критическим определителем Δ() множества . Всякая -допустимая решетка Λ с условием

d(Λ) = Δ()

наз. критической решеткой множества . Для множества бесконечного типа, по определению, Δ() = +∞.

Вычисление постоянной Эрмита γ(F) лучевой функции F сводится к вычислению критич. определителя Δ(_F) звездного тела _F, определяемого условием F(x) < 1:

γ(F) = {Δ(_F)}^-1/n.

Связь между критич. определителем и плотностью плотнейшей решетчатой упаковки устанавливается следующей теоремой Блихфельдта. Пусть - произвольное множество, D - соответствующее ему разностное множество (т. е. совокупность точек ξ - η, где ξ ∈ , η ∈ ) и пусть Λ - решетка. Для того чтобы расположение {, Λ}, т. е. семейство множеств { + а}, где а ∈ Λ, было упаковкой, необходимо и достаточно, чтобы решетка Λ была D-допустимой.

Плотность θ() плотнейшей решетчатой упаковки ограниченного измеримого по Лебегу множества меры V() выражается равенством

θ() = V()/Δ(D).

Для произвольного множества и измеримого по Лебегу множества меры V(), удовлетворяющего условию D ⊂ , справедливо неравенство (другая формулировка теоремы Блихфельдта):

Δ() ≥ V().

Если - выпуклое тело, симметричное относительно точки О, то

Δ() = V()/2ⁿθ(),

где θ() - плотность плотнейшей решетчатой упаковки тела . Так что в случае симметричной выпуклой лучевой функции F(х) вычисление γ(F) сводится к вычислению плотнейшей решетчатой упаковки тела _F, определяемого условием F(х) < 1.

Важнейшим предложением Г. ч. является теорема Минковского о выпуклом теле. Пусть - выпуклое тело, симметричное относительно начала координат и имеющее объем V(). Тогда

Δ() ≥ 2^-nV(). (1)

Иными словами, решетка Λ, для к-рой

V() > 2ⁿd(Λ),

имеет в точку, отличную от 0.

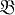Неравенство (1) наз. неравенством Минковского; оно дает оценку снизу для критич. определителя Δ() выпуклого тела , симметричного относительно 0. Эта оценка, вообще говоря, неулучшаема. Для достижения равенства необходимо и достаточно, чтобы θ() = 1. Выпуклые тела , удовлетворяющие условию θ() = 1, наз. параллелоэдрами. Они играют важную роль в Г. ч. и кристаллографии математической.

Все приложения теоремы Минковского о выпуклом теле основаны на том, что для выпуклой симметричной лучевой функции F(х) и произвольной решетки Λ определителя d(Λ) справедливо неравенство

m(F, Λ) ≤ 2{d(Λ)/V(_F)}^1/n,

где

_F = {x | F(x) < 1}.

В частности, для решетки Λ₀ целых точек и лучевой функции

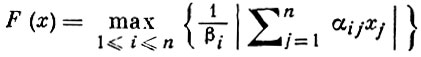
справедлива теорема Минковского о линейных однородных формах. Пусть α_ij, β_i - действительные числа, i, j = 1, ..., n; β_i > 0, |det (α_ij)| = Δ > 0. Если

β₁β₂...β_n > Δ,

то найдутся целые числа x₁, ..., x_n, не равные одновременно нулю и удовлетворяющие системе линейных неравенств

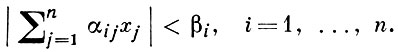
В Г. ч. изучаются последовательные минимумы лучевой функции в решетке. Пусть F(х) - лучевая функция, Λ - решетка и пусть зафиксирован индекс i, 1 ≤ i ≤ n; i-м последовательным минимумом m_i = m_i(F, Λ) функции F в решетке Λ наз. точная нижняя граница чисел μ, для к-рых множество F(х) < μ содержит не менее i линейно независимых точек решетки Λ. При этом

m₁(F, Λ) = m(F, Λ); 0 ≤ m₁ ≤ m₂ ≤ ... ≤ m_n < +∞.

Справедлива оценка

{m₁(F, Λ)}ⁿ Δ(_F)/d(Λ) ≤ 1.

Труднее оценить сверху величину

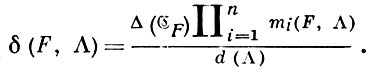
Для этого надо уметь вычислять или оценивать сверху величину

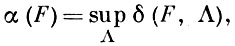
где точная верхняя граница берется по всем n-мерным решеткам Λ. Величина α(F) наз. аномалией лучевой функции F, или аномалией множества _F. Имеет место неравенство α(F) ≥ 1. Оценку α(F) сверху дает (см. [4], с. 254-57) следующая теорема. Пусть F есть n-мерная лучевая функция с аномалией α(F); тогда

α(F) ≤ 2^(n-1)/2.

Построены примеры, показывающие, что эта оценка, вообще говоря, не улучшаема.

Если F - выпуклая симметричная лучевая функция, то предполагается (гипотеза об аномалии выпуклого тела), что

α(F) = 1.

Справедлива вторая теорема Минковского о выпуклом теле, уточняющая первую теорему. Если F(х) - симметричная выпуклая лучевая функция и Λ - решетка, то

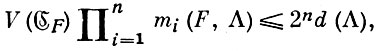
где выпуклое тело _F определяется условием F(х) < 1.

Понятие последовательных минимумов и основные относящиеся к ним результаты (исключая последнюю теорему) обобщаются со звездных тел _F на произвольные множества (см. [9], с. 44 - 46).

Следующее предложение оценивает критич. определитель данного множества сверху: для любого измеримого по Лебегу множества меры V()

Δ() ≤ V(); (2)

при этом, если - симметричное относительно 0 звездное тело, то

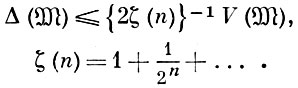
(2)

Все доказательства этой теоремы включают в себя то или иное усреднение нек-рой функции, заданной на пространстве решеток. Наиболее естественный вывод дает (см., напр., [12]) следующая теорема Зигеля о среднем. Пусть f(х) - интегрируемая по Лебегу функция, заданная на n-мерном евклидовом пространстве Rⁿ, а μ - инвариантная мера, заданная на пространстве решеток Λ с определителем =1; ℱ - фундаментальная область этого пространства. Тогда

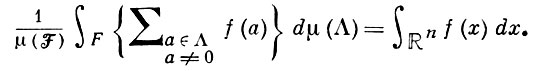
В отличие от оценки снизу (1), оценки (2) и (3) не являются окончательными (уточнение см. [13]).

Оценки критич. определителя Δ() данного множества снизу и сверху приводят к оценкам γ(F) сверху и снизу, т.е. к решению (в известном смысле) однородной задачи Г. ч. Однако часто бывает важно знать и точное значение γ(F) или точное значение критич. определителя Δ() для заданного множества (скажем, для норменного тела данного алгебраического числового поля). Если - заданное ограниченное звездное тело, то, в принципе, можно указать алгоритм, позволяющий свести задачу отыскания всех критич. решеток тела (а следовательно, и Δ()) к конечному числу обычных задач на экстремум нек-рых функций нескольких переменных. Однако этот алгоритм осуществим (при современном состоянии исследований) лишь для выпуклых тел при числе измерений n ≤ 4 (см. [4], с. 185-86, 199-202).

Для неограниченных звездных тел нахождение Δ(), вообще говоря, значительно сложнее; это показывает явление изоляции однородных арифметич. минимумов, состоящее в следующем. Пусть F -лучевая функция в ℝⁿ и пусть на множестве ℒ всех решеток Λ задана величина

μ(Λ) = μ(F, Λ) = m(F, Λ)/{d(Λ)}^1/n.

Множество M(F) возможных значений μ(Λ) для всех Λ ∈ ℒ наз. спектром Маркова лучевой функции F. Говорят, что для F имеет место явление изоляции, если множество М(F) имеет изолированные точки. Множество М(F) лежит на промежутке (0, γ(F)]. Если звездное тело _F, F(x) < 1, ограничено, то

M(F) = (0, γ(F)].

Поэтому явление изоляции возможно лишь для неограниченных звездных тел (см. [4], гл. 10). Наиболее исследован случай n = 2

F₀(x) = |x₁x₂|^1/2. (4)

То, что здесь возникает явление изоляции, впервые заметили (см. [14]) А. Н. Коркин и Е. И. Золотарев (и это был вообще первый пример явления изоляции). А. А. Марковым (1879, см. [14]) доказано, что часть спектра М(F₀), лежащая правее 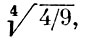, дискретна; она имеет вид

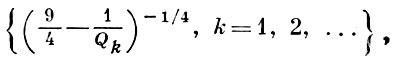
(5)

где Q_k - возрастающая последовательность целых положительных чисел, обладающих тем свойством, что найдутся целые числа R_k, S_k, удовлетворяющие условию

Q²_k + R²_k + S²_k = 3Q_kR_kS_k;

каждой точке спектра (5) («спектр Маркова» в узком смысле) отвечает единственная, с точностью до автоморфизмов (4), решетка Λ_k. Неопределенная форма φ_k = х₁х₂, (х₁, х₂) ∈ Λ_k, иногда наз. формой Маркова, а последовательность φ₁, φ₂, ... наз. цепочкой Маркова. Известно также, что левее нек-рого числа μ₀ = μ₀(F₀) спектр M(F₀) совпадает с отрезком, [0, μ₀]. Явление изоляции можно описать в терминах допустимых решеток (см. [9], с. 50), что несколько обобщает это понятие.

Неоднородная проблема охватывает неоднородные диофантовы задачи, играющие большую роль в теории чисел, она составляет важный раздел Г. ч.

Пусть F - лучевая функция в ℝⁿ, Λ - решетка определителя d(Λ) в ℝⁿ и х₀ - действительная точка в ℝⁿ. Рассматриваются величины

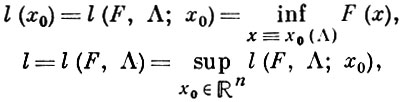
где точная нижняя граница берется по всем точкам вида х+а, а ∈ Λ, а точная верхняя граница берется по всем точкам x₀ ∈ ℝⁿ. Величина l(F, Λ) наз. неоднородным арифметическим минимумом функции F в решетке Λ; при этом «минимум» может и не достигаться. l(F, Λ) есть точная нижняя граница действительных чисел λ > 0, обладающих следующим свойством: расположение {λ_F, Λ} множества λ_F, Λ, где _F удовлетворяет условию F(х) < 1, по решетке Λ является покрытием, т. е.

∪_a∈Λ(λ_F + a) = ℝⁿ.

Для лучевой функции F рассматриваются аналоги постоянной Эрмита:

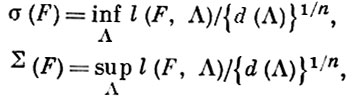
где точная нижняя (верхняя) граница берется по всем n-мерным решеткам Λ. Величина Σ(F) обычно тривиальна (см. [4], с. 369-70): если множество _F, F(х) < 1, имеет конечный объем, то

Σ(F) = +∞.

Однако в одном, представляющем интерес, частном случае функции F, с величиной Σ(F) связана неоднородная проблема Минковского.

Гипотеза Минковского о произведении неоднородных линейных форм. Пусть

F_n(x) = |x₁x₂...x_n|^1/n.

Тогда

Σ(F_n) = 1/2.

Исследования по этой гипотезе и ее аналогам составляют более половины всех исследований по неоднородной проблеме Г. ч. (см. Минковского гипотеза).

В общем случае величина σ(F) носит характер более содержательный, чем Σ(F). Она тесно связана со значением плотности τ(_F) экономнейшего решетчатого покрытия телом _F (см. [7], [10]). Именно, если F -лучевая функция и множество _F ограничено, то

τ(_F) = {σ(F)}ⁿV(_F).

Важный раздел неоднородной проблематики Г. ч. составляют так наз. теоремы переноса для данной лучевой функции F, под к-рыми понимаются неравенства, связывающие неоднородный минимум l(F, Λ) с последовательными однородными минимумами m_i(F, Λ) (или минимумами взаимной функции F* относительно взаимной решетки Λ*, и т. п.) (см. [4], с. 380-90).

Пример: пусть F - симметричная выпуклая лучевая функция и пусть F(x) > 0 для х ≠ 0; тогда для любой решетки Λ

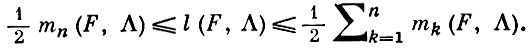
Имеются обобщения Г. ч. на пространства, более общие, чем ℝⁿ, а также на дискретные множества, более общие, чем Λ (см. [15], [10]).

Лит.: [1] Minkowski Н., Geometrie der Zahlen, Lpz.-В., 1953; [2] eго же, Diophantische Approximationen, Lpz., 1907; [3] Hancock H., Development of the Minkowski geometry of numbers, N. Y., 1939; [4] Кассeлс Дж. В. С., Введение в геометрию чисел, пер. с англ., М., 1965; [5] Lekkerkerker С. G., Geometry of numbers, Groningen, 1969; [6] Tот Л. Ф., Расположения на плоскости, на сфере и в пространстве, пер. с нем., М., 1958; [7] Роджерс К., Укладки и покрытия, пер. с англ., М., 1968; [8] Кеllеr О.-Н., Geometrie der Zahlen, Lpz., 1954; [9] Hlawka E., «Jahresber. Dtsch. Math.-Ver.», 1954, Bd 57, Abt. 1, S. 37-55; [10] Барановский E. П., в кн.: Итоги науки. Алгебра. Топология. Геометрия. 1967, М., 1969. с. 189-225; [11] Koksma J. F., Diophantische Approximationen, В., 1936; [12] Macbeath A. M., Rоgers С. А,. «Рrос. Cambridge Philos. Soc.», 1958, v. 54, pt. 2, p. 139-51; [13] Schmidt W., «Ill. J. Math.», 1963, v. 7, № 1, p. 18-23; № 4, p. 714; [14] Марков А. А., «Успехи матем. наук», 1948, т. 3, в. 5, с. 7-51; [15] Rogers К., Swinnerton-Dyer Н. P. F., «Trans. Amer. Math. Soc.», 1958, v. 88, № 1, p. 227-42.

А. В. Малышев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.