ГЕОМЕТРИЧЕСКОЕ ПРИБЛИЖЕНИЕ

ГЕОМЕТРИЧЕСКОЕ ПРИБЛИЖЕНИЕ, геометро-оптическое приближение, - ряд вида

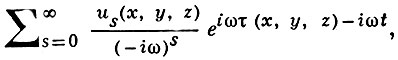
к-рый формально удовлетворяет уравнению, описывающему волновой процесс (или системе уравнений, тогда u_s - векторы).

Для решения краевых задач теории колебаний (см. Дифракции математическая теория) разработан так наз. лучевой метод [2], позволяющий строить Г. п. Существует гипотеза, что получающиеся в результате ряды представляют собой асимптотич. разложение искомых решений там, где члены Г. п. не имеют особенностей. В частных случаях эту гипотезу удалось доказать. Имеется и нестационарный аналог Г. п.

Построение функций u_s основано на рассмотрении поля лучей, т. е. экстремалей функционала (см. Ферма принцип)

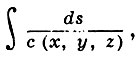
где с(х, у, z) - скорость в рассматриваемой изотропной физич. среде, ds - элемент длины дуги. Пусть пара параметров α, β характеризует луч, параметр τ -точки на луче, причем

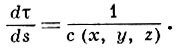
Параметры α, β, τ можно взять за криволинейные координаты. Переход от криволинейных координат α, β, τ к декартовой прямоугольной дается формулой

r(α, β, β) = r(х, у, z).

Поверхности τ = const ортогональны лучам. В тех точках, где поле лучей не имеет особенностей, отлична от нуля величина

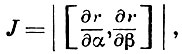
к-рая наз. геометрическим расхождением. Величина J входит в рекуррентные соотношения, связывающие функции u_s между собой, и играет фундаментальную роль во всех построениях Г. п.

Лит.: [1] Фридлендер Ф., Звуковые импульсы, пер. с англ., М., 1962; [2] Бабич В. М., Булдырев В. С., Асимптотические методы в задачах дифракции коротких волн, М., 1972.

В. М. Бабич.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.