ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ

ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ - последовательность чисел, каждое из к-рых равно предыдущему, умноженному на нек-рое постоянное для данной прогрессии число q ≠ 0 (знаменатель прогрессии). Г. п. наз. возрастающей, если q > 1, убывающей, если 0 < q < 1; если q < 0, то Г. п.- знакочередующаяся. Любой член Г. п. а_j выражается через ее первый член а₁ и знаменатель q формулой

a_j = a₁q^j-1,

а сумма первых n членов Г. п. (знаменатель к-рой не равен 1) - формулой

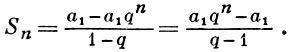
Если |q| < 1 , то при неограниченном возрастании числа n сумма S_n стремится к пределу S = a₁/(1 - q) Это число S наз. суммой бесконечно убывающей геометрической прогрессии.

Выражение

a₁ + a₁q + ... + a₁qⁿ + ..., при |q| < 1,

- простейший пример сходящегося ряда - геометрический ряд, число a₁/(1 - q) является суммой геометрич. ряда.

Термин «Г. п.» связан со свойством любого члена Г. п. с положительными членами:

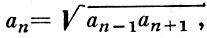
т. е. любой член есть геометрическое среднее между предыдущим и последующим ее членами.

О. А. Иванова.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.