ГЕОДЕЗИЧЕСКИЕ КООРДИНАТЫ

ГЕОДЕЗИЧЕСКИЕ КООРДИНАТЫ в точке Р пространства аффинной связности с объектом связности Г^k_ij - любые координаты, при к-рых в точке Р все Г^k_ij =0. Если равенства Г^k_ij = 0 выполняются во всех точках нек-рой кривой, то говорят о Г. к. вдоль кривой (см. Ферми координаты). В римановом пространстве с метрич. тензором g_ij Г. к. x^k часто определяют условиями

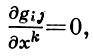
эквивалентными в этом случае условию Г^k_ij = 0. Для симметрич. связности, в частности римановой, существуют Г. к. в любой точке и вдоль любой регулярной дуги кривой без самопересечений. Для поверхности F в евклидовом пространстве Г. к. есть декартовы прямоугольные координаты проекции на касательную к F плоскость; если проектирование вести на развертывающуюся поверхность Q, огибаемую касательными к F плоскостями вдоль кривой, то внутренние декартовы координаты на Q будут координатами Ферми на F.

В Г. к. у ковариантной производной поля тензора в точке Р координаты равны обычным производным от координат тензора. Это можно принять за определение ковариантной производной, следуя идее Э. Картана (Е. Cartan) о перенесении в более общие пространства геометрич. объектов или операций евклидовой геометрии с помощью специальных систем координат, в к-рых в наибольшей степени исключено влияние неевклидовости. На этой же идее основано использование Г. к. в пространстве-времени общей теории относительности, где они связаны с локально инерциальными системами отсяета; их рассмотрение играет заметную роль в физической интерпретации теории.

Геометрически условия Г^k_ij = 0 означают, что прямым xⁱ = ξⁱt (ξⁱ = const, t - параметр) в области изменения координат соответствуют в рассматриваемом пространстве кривые γ(t), имеющие в точке Р нулевой вектор

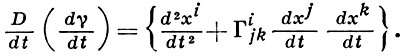
Если Г. к. таковы, что прямым всех направлений в точке Р соответствуют геодезические, на к-рых повсюду D/dt(dγ/dt), то хⁱ наз. римановыми координатами.

Ю. А. Волков.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.