ГЕОДЕЗИЧЕСКАЯ ОКРУЖНОСТЬ

ГЕОДЕЗИЧЕСКАЯ ОКРУЖНОСТЬ - множество точек метризованного двумерного многообразия, удаленных на расстояние r от фиксированной точки О. Частный случай сферы в метрич. пространстве.

На регулярной поверхности и вообще в двумерном римановом пространстве Г. о. при малых r есть простая замкнутая кривая (не обязательно постоянной геодезической кривизны); в каждую ее точку идет из О единственная кратчайшая (радиус), с к-рой Г. о. образует прямой угол; Г. о. ограничивает выпуклую область. При r → 0 длина l Г. о. связана с гауссовой кривизной К в точке О соотношением

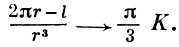
При больших r в точки Г. о. может идти более одного радиуса, она может ограничивать невыпуклую область, распадаться на отдельные компоненты. Г. о. часто используют в исследованиях по геометрии в целом. Свойства Г. о. изучались на общих выпуклых поверхностях и в нерегулярно метризованных многообразиях (см. [1]).

Г. о. в смысле Дарбу - замкнутая кривая постоянной геодезич. кривизны. Является стационарной кривой для изопериметрич. задачи. На поверхностях постоянной кривизны совпадает с Г. о. в обычном смысле (см. [2]).

Лит.: [1] Бураго Ю. Д., Стратилатова М. Б., «Тр. матем. ин-та АН СССР», 1965, т. 76, с. 88-114; [2] Бляшке В., Дифференциальная геометрия и геометрические основы теории относительности Эйнштейна, пер. с нем., М.-Л., 1935.

В. А. Залгаллер.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.