ГЕОДЕЗИЧЕСКАЯ ЛИНИЯ

ГЕОДЕЗИЧЕСКАЯ ЛИНИЯ, геодезическая,- геометрическое понятие, обобщающее понятие прямой (или отрезка прямой) евклидовой геометрии на случай пространств более общего вида. Определения Г. л. в различных пространствах зависят от того, какая из структур (метрика, линейный элемент, линейная связность) лежит в основе геометрии рассматриваемого пространства. В геометрии тех пространств, где метрика считается заданной априори, Г. л. определяют как локально кратчайшие. В пространствах со связностью Г. л. определяют как кривые, у к-рых касательный вектор остается касательным при параллельном перенесении вдоль кривой. В римановой и финслеровой геометриях, где первоначально задается линейный элемент (иначе говоря,- метрика в касательном пространстве в каждой точке рассматриваемого многообразия), а длины кривых получаются последующим интегрированием, Г. л. определяют как экстремали функционала длины кривой.

Впервые Г. л. изучались И. Бернулли (J. Bernoulli) и Л. Эйлером (L. Euler) при отыскании кратчайших на регулярных поверхностях в евклидовом пространстве. На таких линиях обращается в нуль геодезическая кривизна; главная нормаль этих кривых параллельна нормали к поверхности. При изгибаниях Г. л. сохраняются. Движение консервативной механич. системы с конечным числом степеней свободы описывается Г. л. в соответственно подобранном римановом пространстве.

В римановых пространствах Г. л. изучены наиболее полно. Пусть Мⁿ есть n-мерное риманово пространство с метрич. тензором g_ij класса С^k, k ≥ 2. Определение Г. л. как экстремали позволяет написать ее дифференциальные уравнения в произвольных локальных координатах хⁱ, i = 1, 2, ..., n, при любой параметризации γ = {xⁱ(t)}:

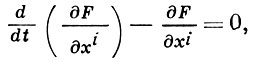
где

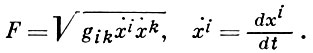
Другая эквивалентная форма уравнений Г. л. выводится из требования параллельности переноса вдоль γ касательного вектора γ̇ = {х̇ⁱ}. Если t есть длина s дуги вдоль Г. л. или линейная функция от s, то

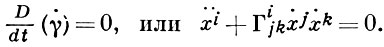
(1)

Определение Г. л. уравнением (1) включает и канонич. выбор параметра. При таком определении через каждую точку х₀ проходит Г. л. γ = x(t, ξ) с начальным касательным вектором ξ, х(0, :) = х₀, х̇(0, ξ) = ξ. Отображение ξ → х(1, ξ) касательного пространства в точке х₀ в изучаемое пространство есть экспоненциальное отображение с полюсом х₀. Вблизи начальной точки х₀ -диффеоморфизм, вводящий в изучаемом пространстве римановы координаты.

Ряд свойств Г. л. сохраняется у кривых, определяемых уравнениями 2-го порядка ẍ = F(х, х̇), если, подобно (1), функция F - однородная 2-й степени по {х̇ⁱ}. Определение таких уравнений в терминах касательных расслоений приводит к понятиям пульверизации и их интегральных кривых. Частным случаем последних являются Г. л. (см. [2]).

Поведение Г. л. в малом похоже на поведение прямых в евклидовом пространстве. Достаточно малая дуга Г. л. является кратчайшей среди всех спрямляемых кривых с теми же концами. Через любую точку в любом направлении проходит единственная Г. л. У каждой точки есть окрестность U, в к-рой любые две точки соединимы единственной Г. л., не выходящей из U (см. [3]).

Вопрос о том, как далеко можно продолжить из точки х₀ дугу Г. л., чтобы она оставалась кратчайшей по сравнению с близкими к ней кривыми, составляет одну из задач вариационного исчисления. Сравнение Г. л. с близкими кривыми основано на изучении второй вариации длины, к-рая исследуется путем рассмотрения поля скоростей (Якоби поле) в точках Г. л. γ(s) при варьировании γ(s, t). При любом фиксированном t кривая γ(s, t) остается геодезической, а параметр s на ней - каноническим. Если в начале кривой γ скорость равна нулю, то те точки кривой γ, где эта скорость при каком-либо ненулевом поле Якоби оказывается нулем, наз. сопряженными точками. Г. л. остается кратчайшей по сравнению с близкими кривыми до первой сопряженной точки. Для дуги Г. л., продолженной за сопряженную точку, существует сколь угодно близкая более короткая кривая с теми же концами. Поле Якоби η(s) удовлетворяет уравнению

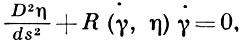
где γ̇ - касательный вектор геодезической γ(s), а R(γ̇, η) - кривизны преобразование, или, в координатах Ферми хⁱ, x¹ = s:

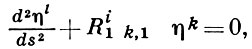
(2)

где R^l_{i j,k} - тензор кривизны. Связь поля Якоби с кривизной обусловливает зависимость свойств геодезических от кривизны пространства. Напр., в пространствах отрицательной кривизны сопряженных точек нет; если пространство еще и односвязно, то любая дуга Г. л.- кратчайшая, а выходящие из точки Г. л. экспоненциально расходятся. Эти свойства играют роль в теории динамич. систем (см. Геодезический поток). Монотонность влияния кривизны является предметом ряда так наз. теорем сравнения. В частности, расстояние до первой сопряженной точки и длины векторов поля Якоби на этом участке (нормированных требованием η(0) = 0, |Dη/ds| = 1) убывают с ростом кривизны пространства. Здесь подразумевается сравнение двух Г. л., в соответствующих по длине точках к-рых все кривизны второго пространства мажорируют любую из кривизн первого пространства [4].

В общей теории относительности уравнение (2) служит источником физического истолкования кривизны пространства-времени через поведение Г. л. (см. [5]).

При отказе от сравнения только с близкими кривыми дуга Г. л. может перестать быть кратчайшей раньше, чем пройдет сопряженную точку. Это возможно даже в односвязном пространстве, т. е. причины этого могут быть топологическими и метрическими.

Вопрос о том, как влияет кривизна на протяженность дуги, на к-рой Г. л. остается кратчайшей, играет существенную роль в изучении связей кривизны с топологич. строением пространства. Зависимость количества замкнутых Г. л. или количества разных Г. л., соединяющих две точки, от топологич. строения пространства составляет предмет вариационного исчисления в целом (см. [6], [4], [7]).

Семейства Г. л., рассматриваемые как возможные траектории движения, являются предметом теории динамич. систем и эргодич. теории.

В пространствах аффинной связности Г. л. определяются уравнением (1). Для них сохраняются локальные теоремы существования и единственности Г. л., соединяющих две точки, и существования выпуклой окрестности.

Г. л. с аналогичными свойствами определяются и в пространствах проективной связности, а также в случае более общих связностей на многообразиях.

Геометризация задач вариационного исчисления для функционалов, отличных от длины кривой, привела к понятию финслерова пространства и Г. л. в нем. Выделение основных геометрических свойств подобных пространств привело к понятию геодезических геометрии, которое определяется наличием и продолжаемостью Г. л.

Из метрич. пространств с нерегулярной метрикой наиболее изучены Г. л. на выпуклых поверхностях и в двумерных многообразиях ограниченной кривизны. Здесь Г. л. не обязательно гладкая кривая; Г. л. может не иметь продолжения, а в двумерном многообразии ограниченной кривизны может также иметь неединственное продолжение. Г. л. на выпуклой поверхности всегда имеют полукасательную; если продолжается, то только единственным образом; из точки Г. л. исходят почти во всех направлениях. В таких пространствах более естественным, чем Г. л., оказался класс квазигеодезических линий, к-рые служат замыканием класса геодезических (см. [8]).

Лит.: [1] Pашевский П. К., Риманова геометрия и тензорный анализ, 3 изд., М., 1967; [2] Ленг С., Введение в теорию дифференцируемых многообразий, пер. с англ., М., 1967; [3] Хелгасон С., Дифференциальная геометрия и симметрические пространства, пер. с англ., М., 1964; [4] Громол Д., Клингенберг В., Мейер В., Риманова геометрия в целом, пер. с нем., М., 1971; [5] Синг Дж. Л., Общая теория относительности, пер. с англ., М., 1963; [6] Люстерник Л. А., Шнирельман Л. Г., Топологические методы в вариационных задачах, М., 1930; [7] Милнор Дж., Теория Морса, пер. с англ., М., 1963; [8] Александров А. Д., Внутренняя геометрия выпуклых поверхностей, М.-Л., 1948.

Ю. А. Волков.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.