ГЕНЦЕНА ФОРМАЛЬНАЯ СИСТЕМА

ГЕНЦЕНА ФОРМАЛЬНАЯ СИСТЕМА - логико-математич. исчисление, служащее для формализации и исследования содержательных доказательств, оперирующих с допущениями (гипотезами). Введены Г. Генценом (G. Gentzen, [2]). Г. ф. с. делят на системы естественного вывода (или натуральные, имитирующие форму обычных математич. умозаключений и потому особенно подходящие для формализованной записи их) и секвенциальные (или логистические, направленные на анализ возможных доказательств данной формулы, на получение результатов о нормальной форме доказательств и их использование в доказательств теории и в теории доказательства теорем на ЭВМ). Иногда Г. ф. с. отождествляют с системами секвенциального типа; тем не менее натуральные Г. ф. с. могут использовать секвенции, а секвенциальные Г. ф. с. иногда оформляют в виде исчисления формул, а не секвенций; иногда все Г. ф. с. считают натуральными, т. к. все они в той или иной степени отражают обычные приемы оперирования с логич. связками и допущениями.

Натуральные Г. ф. с. содержат правила введения логич. символов и правила удаления символов. Логич. аксиомы немногочисленны (обычно одна - две). Напр., натуральный вариант классич. исчисления предикатов для языка {∀, ⊃, ¬} задается аксиомой А → А, правилами введения

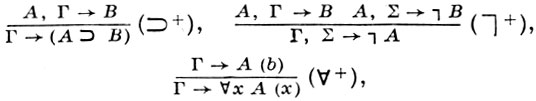
где b не входит в Г и ∀х А(х); правилами удаления

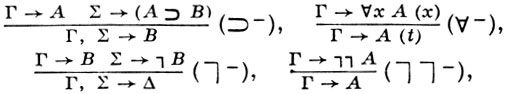
где t - произвольный терм, и структурными правилами:

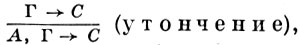
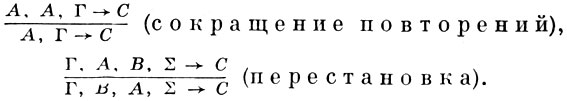
Секвенция, находящаяся под чертой, наз. заключением правила, а секвенции, находящиеся над чертой,- посылками. Аксиома А → А изображает введение допущения А; правило (⊃⁺) иллюстрирует освобождение от допущения: формула В верхней секвенции зависит от допущения А, формула A ⊃ B нижней секвенции уже не зависит от А. Г. ф. с. натурального типа задается иногда в виде исчисления формул (а не секвенций) с неявной записью зависимости от допущений: вывод в таком исчислении - это древовидный граф, в вершинах к-рого могут находиться произвольные формулы (не обязательно аксиомы), а все переходы производятся по правилам вывода. Эти правила получаются вычеркиванием антецедентов из соответствующих правил натуральной системы, описанной с помощью секвенций, причем в случае, когда происходит освобождение от допущений, добавляются соответствующие условия, напр.

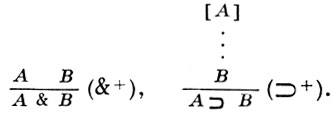
Считается, что вхождение V формулы в такой вывод зависит от допущения D, если D не является аксиомой, находится на вершине вывода над V, и в ветви, ведущей от рассматриваемого вхождения D к V, не происходит освобождения от допущения D. При истолковании такого вывода каждому вхождению формулы С сопоставляется секвенция Г → C, где Г - полный список допущений, от которых зависит рассматриваемое вхождение формулы С. Связь натуральных Г. ф. с. с обычными (гильбертовскими) вариантами соответствующих систем устанавливается с помощью утверждения: Г → С выводимо в натуральной системе тогда и только тогда, когда С выводимо из Г с фиксированными переменными в обычной системе.

Натуральные Г. ф. с. в их первоначальной форме плохо приспособлены для поиска вывода путем анализа: при попытке выяснить, по какому правилу из каких посылок могла получиться данная формула (секвенция), возникает неоднозначность - в принципе это может быть правило введения соответствующей логич. связки или любое из правил удаления. При этом множество возможных посылок в правилах удаления потенциально неограничено (за счет варьирования формулы А в правиле (⊃^-)). Поэтому полезно иметь правила, обладающие свойством подформульности: в посылки входят только подформулы заключения, а бесконечность проявляется лишь за счет варьирования вида термов в правилах типа (∀^-). В секвенциальных Г. ф. с. либо все правила обладают свойством подформульности, либо это свойство нарушается лишь для одного правила - правила сечения:

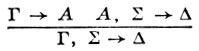
или другого правила близкого вида, напр. для правила (¬^-). Поэтому Г. ф. с, обладающие свойством подформульности, наз. также свободными от сечения или Г. ф. с. без сечения.

Пример. Свободный от сечения вариант классич. исчисления предикатов LK. Выводимые объекты -произвольные секвенции, составленные из {⊃, ¬, А}-формул. Аксиома A → A.

Сукцедентные правила:

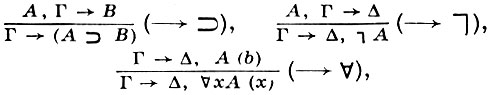
где b не входит в Г и ∀х А(х).

Антецедентные правила:

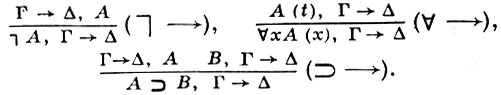
Структурные правила: сечение, перестановка, утончение и сокращение повторений в антецеденте и сукцеденте (см. Секвенция).

При сравнении секвенциальных и натуральных Г. ф. с. правилам введения соответствуют сукцедентные правила, правилам удаления - антецедентные правила. При моделировании в секвенциальных Г. ф. с. правил удаления используется сечение. Свойство подформульности для LK обеспечивает основная теорема Генцена (теорема об устранимости сечения): по всякому выводу в LK можно построить вывод (той же секвенции) без сечения. Эта теорема позволяет устанавливать разрешимость бескванторных систем: из подформул данной бескванторной формулы можно составить лишь конечное число несходных секвенций (секвенции сходны, если они отличаются лишь порядком и повторениями членов в антецеденте и сукцеденте), из к-рых, в свою очередь, можно составить лишь конечное число «кандидатов» в выводы; данная формула доказуема, если среди этих кандидатов найдется вывод.

Г. ф. с. позволяют отражать содержательные особенности теории с помощью чисто структурных соображений; так, Г. ф. с. конструктивной математики часто отличаются от соответствующих классич. систем лишь использованием односукцедентных секвенций вместо произвольных. В свободных от сечения системах легко доказывается непротиворечивость (т. е. невыводимость пустой секвенции), а также выводимость одного из дизъюнктивных членов выводимой дизъюнкции.

Важным обобщением Г. ф. с. являются полуформальные системы, содержащие правила с бесконечным множеством посылок, напр. правило бесконечной индукции (ω-правило):

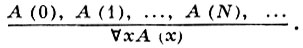
Лит.: [1]Клини С. К., Введение в метаматематику, пер. с англ., М., 1957; [2] Генцен Г., в кн.: Математическая теория логического вывода, Сб. переводов, М., 1967, с. 9-76; [3] Карри X. Б., Основания математической логики, пер. с англ., М., 1969; [4] Рrawitz D., Ideas and results in proof theory, в кн.: Proc. 2 Scand. logic symposium, Amst.- L., 1971.

Г. E. Минц.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.