ГЕЛЬМГОЛЬЦА УРАВНЕНИЕ

ГЕЛЬМГОЛЬЦА УРАВНЕНИЕ - уравнение с частными производными вида

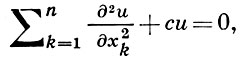
где с - постоянное число. К Г. у. приводит изучение установившихся колебательных процессов. При с = 0 Г. у. переходит в Лапласа уравнение. В случае, если в правой части Г. у. стоит функция f{x), это уравнение наз. неоднородным Г. у.

Для Г. у., являющегося уравнением эллиптич. типа, в ограниченной области ставятся обычные краевые задачи (Дирихле, Неймана и др.). Те значения с, для к-рых существует не равное тождественно нулю решение однородного Г. у., удовлетворяющее соответствующему однородному краевому условию, наз. собственным значением оператора Лапласа (соответствующей краевой задачи). В частности, для задачи Дирихле все собственные значения положительны, а для задачи Неймана - неотрицательны. Для значений с, совпадающих с собственными значениями, решение краевой задачи для Г. у. заведомо неединственно. Если же значения с отличны от собственных, то теорема единственности справедлива.

При решении краевых задач для Г. у. применяются обычные методы теории эллиптич. уравнений (сведение к интегральному уравнению, вариационный метод, метод конечных разностей).

В случае неограниченной области с компактной границей для Г. у. ставятся внешние краевые задачи, к-рые при с < 0 имеют единственное решение, стремящееся к нулю на бесконечности. При с > 0 стремящееся к нулю на бесконечности решение Г. у., вообще говоря, не является единственным. В этом случае для выделения единственного решения ставят дополнительные условия (см. Внешняя и внутренняя краевые задачи, Предельного поглощения принцип).

Для регулярного в области G решения Г. у. справедлива следующая формула среднего значения

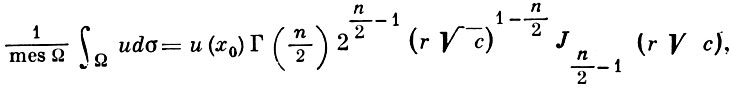
где Ω - сфера радиуса r с центром в точке х₀, целиком лежащая в области G, J_ν(х) - Бесселя функция порядка ν.

Г. у. рассматривалось Г. Гельмгольцем (Н. Helmholtz), к-рый получил первые теоремы о решении краевых задач для этого уравнения в 1860.

Лит.: [1] Курант Р., Гильберт Д., Методы математической физики, пер. с нем., т. 1 (3 изд.), т. 2 (2 изд.), М.-Л., 1951; [2] Тихонов А. Н., Самарский А. А., Уравнения математической физики, 3 изд., М., 1966.

Ш. А. Алимов, В. А. Ильин.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.