ГЁЛЬДЕРОВО ПРОСТРАНСТВО

ГЁЛЬДЕРОВО ПРОСТРАНСТВО - банахово пространство ограниченных и непрерывных функций f(x) = f(х¹, х², ..., хⁿ), определенных на множестве Е n-мерного евклидова пространства и удовлетворяющих на Е Гёльдера условию.

Г. п. С_m(Е), m ≥ 0 - целое, состоит из m раз непрерывно дифференцируемых на Е функций (непрерывных при m = 0).

Г. п. С_m+α(Е), 0 < α ≤ 1, m ≥ 0 - целое, состоит из функций, m раз непрерывно дифференцируемых (непрерывных при m = 0), все m-е производные к-рых удовлетворяют условию Гёльдера с показателем α.

Норма в С_m(Е) и С_m+α(Е) вводится следующим образом:

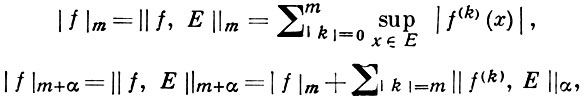
где k = (k₁, k₂, ..., k_n), k_j ≥ 0 - целые,

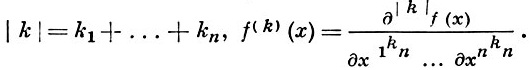
Основные свойства Г. п. для ограниченной связной области (E̅ - замыкание E):

1) C_m+β(E̅) вложено в C_k+α(E̅), если 0 ≤ k + α ≤ m + β, k, m - целые, 0 < α ≤ 1, 0 ≤ β ≤ 1. При этом |f|_k+α ≤ A|f|_m+β и постоянная А не зависит от f ∈ С_m+β(Е̅).

2) Единичный шар пространства С_m+β(Е̅) компактен в С_m+α(Е̅), если 0 < α < β. Следовательно, любое ограниченное множество функций из С_m+β(Е̅) содержит последовательность функций, сходящихся в метрике C_m+α(E̅) к функции пространства C_m+α(E̅).

Лит.: [1] Миранда К., Уравнения с частными производными эллиптического типа, пер. с итал., М., 1957.

Л. П. Купцов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.