ГЁЛЬДЕРА УСЛОВИЕ

ГЁЛЬДЕРА УСЛОВИЕ - неравенство, в к-ром приращение функции оценивается через приращение ее аргумента. Функция f(x), определенная в области Е n-мерного евклидова пространства, удовлетворяет в точке у ∈ Е Г. у. с показателем α (порядка α), где 0 < α ≤ 1, и коэффициентом А(у), если

|f(x) - f(y)| ≤ A(y) |x - y|^α (1)

для всех х ∈ Е, достаточно близких к у. Это Г. у. наз. иногда изотропным Г. у. Говорят, что f(x) удовлетворяет на множестве E' ⊂ E (изотропному) Г. у. с показателем α, если Г. у. (1) выполнено для всех у ∈ Е'. В случае, когда

А = sup_y∈E А(у) < ∞,

Г. у. наз. равномерным на Е, а А - коэффициентом Гёльдера функции f(х) на Е. Г. у. наз. также непрерывностью по Гёльдеру. Величина

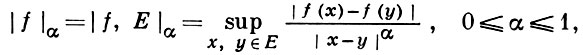
наз. α-полунормой Гёльдера ограниченной функции на множестве Е. Полунорма Гёльдера, как функция от f, логарифмически выпукла:

|f|_αt+β(1-t) ≤ |f|^t_α |f|^1-t_β.

Неизотропное Г. у. вводится аналогично Г. у. (1) и имеет вид:

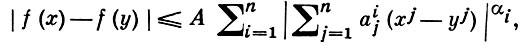
где 0 < α_i ≤ 1, a det (а^j_i) ≠ 0. Функции, удовлетворяющие неизотропному Г. у., непрерывны и имеют по направлению ковектора aⁱ = (аⁱ₁, аⁱ₂, ..., аⁱ_n) показатель Гёльдера α_i, 1 ≤ i ≤ n.

Для числовых функций одного действительного переменного условие вида (1) было введено Р. Липшицем (В. Lipschitz, 1864) в связи с исследованиями по тригонометрич. рядам. В этом случае Г. у. часто наз. условием Липшица порядка α с константой Липшица А. Для числовых функций n(≥2) действительных переменных Г. у. было введено O. Гёльдером (О. Hölder) при исследовании дифференциальных свойств ньютонова потенциала.

Г. у. естественным образом переносится на случай отображений метрич. пространств. Говорят, что отображение f: Х → Е метрич. пространства X в метрич. пространство Е удовлетворяет в точке х₀ ∈ Х Г. у. с показателем α и коэффициентом А(х₀), если существует такая окрестность U(x₀) ⊂ X точки х₀, что для любого x ∈ U(x₀) выполняется неравенство

ρ_E(f(x), f(x₀)) ≤ А(x₀) ρ^α_X(х, х₀).

Здесь ρ_X и ρ_E - метрики пространств X и Е. Аналогично вводится Г. у. на множестве X' ⊂ X, равномерное на X Г. у. и α - полунормы Гёльдера.

Векторные пространства функций, удовлетворяющих тому или иному Г. у., образуют Гёльдерово пространство.

Л. П. Купцов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.