ГЁЛЬДЕРА МЕТОДЫ СУММИРОВАНИЯ

ГЁЛЬДЕРА МЕТОДЫ СУММИРОВАНИЯ - совокупность методов суммирования числовых рядов; введены О. Гёльдером [1] как обобщение средних арифметических метода суммирования. Ряд

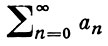
суммируется методом Гёльдера (H, k) к сумме s, если

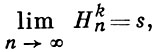
где

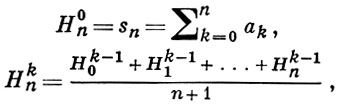
k = 1, 2, ... В частности, (H, 0)-суммируемость ряда означает его обычную сходимость; (H, 1) есть метод средних арифметических. Методы (H, k) - вполне регулярные методы суммирования при любом k и совместны для всех k (см. Совместность методов суммирования). С увеличением k сила метода возрастает: если ряд суммируем методом (H, k) к сумме s, то он суммируем к той же сумме методом (H, k') при любом k' > k. Метод (H, k) при всех k равносилен и совместен с Чезаро методом суммирования того же порядка k. Если ряд суммируем методом (H, k), то его члены аⁿ необходимо удовлетворяют условию аⁿ = о(n^k).

Лит.: [1] Hölder О., «Math. Ann.», 1882, Bd 20, S. 535-549; [2] Xapди Г., Расходящиеся ряды, пер. с англ., М., 1951.

И. И. Волков.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.