ГЕЙЗЕНБЕРГА ПРЕДСТАВЛЕНИЕ

ГЕЙЗЕНБЕРГА ПРЕДСТАВЛЕНИЕ - одно из основных возможных (наряду с Шрёдингера представлением и взаимодействия представлением) эквивалентных представлений зависимости от времени t операторов А и волновых функций Ψ в квантовой механике и квантовой теории поля. В Г. п. операторы А_H зависят от t, а волновые функции ψ_H не зависят от t, и связаны с соответствующими не зависящими от t операторами A_s и зависящими от t волновыми функциями ψ_s(t) в представлении Шрёдингера унитарным преобразованием

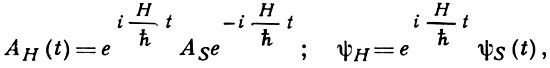
(1)

где эрмитов оператор H есть полный гамильтониан системы, не зависящий от времени. Возможность введения Г. п., как и представления Шрёдингера и взаимодействия, и их эквивалентность основаны на том, что являются наблюдаемыми и имеют физич. смысл не сами по себе А или ψ, а лишь среднее значение операторов А в состоянии ψ, к-рое должно быть инвариантно относительно унитарных преобразований типа (1) и, следовательно, не должно зависеть от выбора представления. Дифференцирование (1) по t дает уравнение для операторов A_H(t) в Г. п., к-рое содержит всю информацию об изменении состояния квантовой системы с течением времени t:

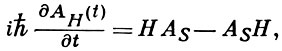
где операторы H и A_s, вообще говоря, не коммутируют.

Г. п. названо по имени В. Гейзенберга (W. Heisenberg), к-рый ввел его в 1925 в матричной формулировке квантовой механики.

В. Д. Кукин.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.