ГАУССОВСКИЙ ПРОЦЕСС

ГАУССОВСКИЙ ПРОЦЕСС - действительный случайный процесс X = X(t), t ∈ T, любые конечномерные распределения к-рого являются гауссовскими, т. е. характеристич. функции совместных распределений вероятностей случайных величин X(t₁), ..., X(t_n) при любых t₁, ..., t_n ∈ T имеют вид:

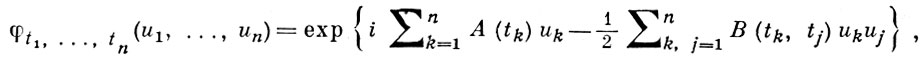
где A(t) = EX(t) - математич. ожидание и

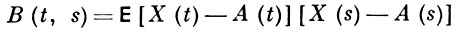
- корреляционная функция. Распределение вероятностей Г. п. Х = X(t) полностью задается его математич. ожиданием A(t) и корреляционной функцией В(t, s), s, t ∈ T. Для любой функции A (t) и любой положительно определенной функции В (t, s) существует Г. п. X(t), у к-рого среднее значение и корреляционная функция суть именно A(t) и В(t, s). Многомерный случайный процесс с векторными значениями

X(t) = (X₁(t), ..., X_m(t)}

наз. гауссовским, если гауссовскими являются совместные распределения вероятностей любых величин

Х_i1(t₁), ..., X_in(t_n).

Комплексным Г. п. X = X (t), t ∈ T, наз. случайный процесс вида

X(t) = X₁(t) + X₂(t),

где действительные X₁(t), X₂(t) в совокупности образуют двумерный Г. п. Иногда, говоря о комплексном Г. п. X(t) = X₁(t) + iX₂(t) считают, что выполняется одно дополнительное условие:

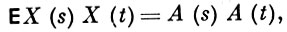
где

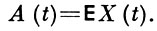
Это условие вводится для того, чтобы сохранить то свойство обычных гауссовских случайных величин, согласно к-рому некоррелированность равносильна независимости; его можно переписать следующим образом:

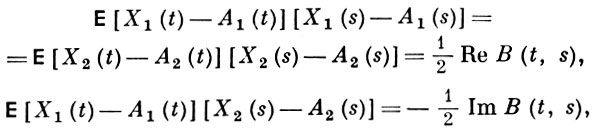
где _

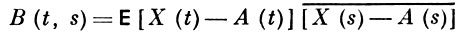
- корреляционная функция процесса X(t) и

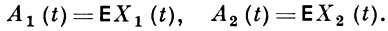
Действительный обобщенный случайный процесс X = 〈u, X〉, u ∈ U, на линейном пространстве U наз. обобщенным Г. п., если его характеристич. функционал φ_X(u) имеет вид:

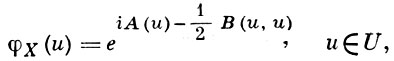
где А(u) = Е 〈u, Х〉 - математич. ожидание обобщенного процесса Х = 〈u, X〉,

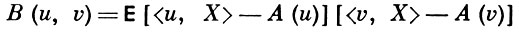
- его корреляционный функционал.

Пусть U - гильбертово пространство со скалярным произведением (u, v), u, v ∈ U. случайная величина X со значениями в пространстве U наз. гауссовской, если случайный процесс вида Х = 〈u, X〉, u ∈ U, -обобщенный Г. п. Математич. ожидание А(u) является линейным непрерывным функционалом, а корреляционная функция В(u, v) - билинейным непрерывным функционалом на гильбертовом пространстве U, причем

В(u, v) = (Вu, v), u, v ∈ U,

где положительный оператор В - корреляционный оператор случайной величины X ∈ U, является ядерным. Для любых таких А (u) и В (u, v) существует гауссовская величина X ∈ U такая, что обобщенный процесс Х = 〈u, X〉, u ∈ U, имеет средним значением и корреляционной функцией именно А(u) и В(u, v).

Пример. Пусть X = X(t) - Г. п. на отрезке Т = [а, b] и пусть процесс X(t) измерим, причем

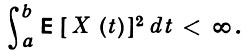
Тогда почти все траектории X(t), t ∈ T, будут принадлежать пространству интегрируемых в квадрате функций u = u(t) на отрезке Т со скалярным произведением

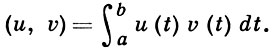
Формула

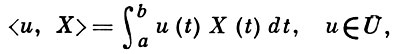
задает обобщенный Г. п. на этом пространстве U. При этом математич. ожидание и корреляционный функционал обобщенного процесса Х = 〈u, X〉 выражаются формулами:

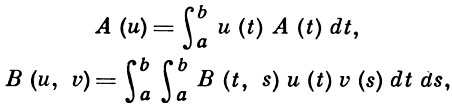
где A(t) и В(t, s) - соответствующие математич. ожидание и корреляционная функция исходного процесса X = X(t) на отрезке T = [а, b].

Почти все основные свойства Г. п. X = X(t) (параметр t пробегает произвольное множество Т) могут быть выражены в геометрич. терминах при рассмотрении этого процесса как кривой в гильбертовом пространстве Н всех случайных величин Y, ЕY² < ∞, со скалярным произведением (Y₁, Y₂) = EY₁Y₂, для к-рой

(X(t), 1) = А (t)

и

(X(t) - A(t), X(s) - A(s)) = B(t, s).

Ю. А. Розанов.

Стационарные в узком смысле Г. п. могут быть реализованы посредством нек-рых динамич. систем (сдвиг в пространстве траекторий, см. [1]). Полученные динамич. системы (их иногда наз. нормальными, сравни с нормальным распределением вероятностей) представляют интерес как примеры динамич. систем с непрерывным спектром, свойства к-рых благодаря упомянутому разложению Н могут быть изучены с большой полнотой. Так были построены первые конкретные примеры динамич. систем с «неклассическими» спектральными свойствами.

Д. В. Аносов.

Лит.: [1] Дуб Дж. Л., Вероятностные процессы, пер. с англ., М., 1956; [2] Ибрагимов И. А., Розанов Ю. А., Гауссовские случайные процессы, М., 1970; [3] Крамер Г., Лидбеттер М., Стационарные случайные процессы. Свойства выборочных функций и их приложения, пер. с англ., М., 1969; [4] Itô K., «J. Math. Soc. Japan», 1951, v. 3, № 1, p. 157-69; [5] его же, «Japan. J. Math.», 1952, v. 22, p. 63-86.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.