ГАУССА-БОННЕ ТЕОРЕМА

ГАУССА-БОННЕ ТЕОРЕМА: полная кривизна ω двумерного компактного риманова многообразия V², замкнутого или с краем, и поворот τ его гладкого края (границы) ∂V² связаны с эйлеровой характеристикой χ многообразия V² соотношением

ω + τ = 2πχ;

здесь

ω = ∫_V² KdS,

где K - гауссова кривизна, a S - площадь;

τ = ∫_∂V² k_g dl,

где k_g - геодезич. кривизна, а l - длина границы. Г. - Б. т. справедлива и для многообразия с кусочно | гладкой границей, в этом случае

τ = ∫k_gdl + ∑_i(π - α_i),

где π - α_i есть поворот границы в угловой точке. В частности, теорема справедлива на регулярных поверхностях в Е³. К Г.-Б. т. близко подошел К. Гаусс (см. [1]), в отчетливой форме (для гомеоморфных кругу поверхностей) она опубликована О. Бонне (см. [2]).

Для некомпактного полного V² без края аналогом Г.-Б. т. является неравенство Кон-Фоссена (см. [3]):

∫_V² K dS ≤ 2πχ.

Г.-Б. т. и приведенное неравенство верны также для выпуклых поверхностей и двумерных многообразий ограниченной кривизны.

Г.-Б. т. обобщается для четномерных компактных римановых многообразий V^2p, замкнутых или с краем:

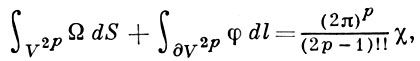
где S, l - объемы в V^2p и ∂V^2p, Ω - нек-рый полином от компонент тензора кривизны V^2p, φ - нек-рый полином от компонент тензора кривизны и коэффициентов второй квадратичной формы ∂V^2p (см. [4]). Г.-Б. т. распространена также на римановы полиэдры [5]. Другие обобщения Г.-Б. т. связаны с интегральными представлениями характеристич. классов через параметры римановой метрики (см. [4], [6], [7]).

Лит.: [1] Gauss С., Werke, Bd 8, Gütt., 1900; [2] Bonnet О., «J. École polytech.», 1948, t. 19, p. 1-146; [3] Кон-Фосceн С. Э., Некоторые вопросы дифференциальной геометрии в целом, М., 1959; [4] ШарафутдиновВ. А., «Сиб. матем. ж.», 1973 , т. 14, № 6, с. 1321-35; [5] Аllеndоеrfer С. В., Weil A., «Trans. Amer. Math. Soc.», 1943, v. 53, № 1, p. 101-29; [6] Eells J., «Trans. Amer. Math. Soc.», 1959, v. 92, № 1, p. 142-53; [7] Понтpягин Л. С., «Изв. АН СССР. Сер. матем.», 1949, т. 13, № 2.

Ю. Д. Бураго.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.