ГАУССА СУММА

ГАУССА СУММА - тригонометрическая сумма вида

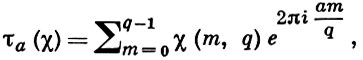
где χ(m, q) - числовой характер по модулю q. Г. с. вполне определяется заданием характера χ(m, q) и числа а. Г. с. были рассмотрены К. Гауссом (С. Gauss) в 1811 в случае простого нечетного q = p и характера χ(m, q) = (m/q) где (m/q) - Лежандра символ. В этом случае

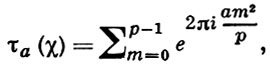
где (а, р) = 1. Исследуя свойства суммы (*) К. Гаусс нашел точное выражение для модуля этой суммы:

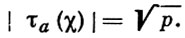
Он также решил более трудную задачу определения знака τ_a(χ) и показал, что

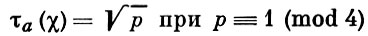
и

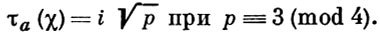
К. Гаусс использовал свойства сумм (*) для решения нек-рых задач теории чисел, в частности он применил их в одном из доказательств квадратичного закона взаимности.

Значение Г. с. для теории чисел было выявлено только в 20-е гг. 20 в. В это время Г. Вейль (Н. Weyl) применил для исследования равномерных распределений более общие тригонометрич. суммы, получившие назв. Вейля сумм. В то же время И. М. Виноградов использовал Г. с. для получения оценки сверху наименьшего квадратичного невычета по модулю р.

Г. с. позволяют установить связь между двумя важными объектами теории чисел: между мультипликативными характерами χ = χ(m, p) и аддитивными характерами

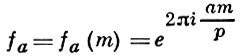
(ради простоты берется только случай простого модуля р). Множество F всех комплекснозначных функций f(x) периода р образует р-мерное векторное пространство над полем комплексных чисел. Если определить скалярное произведение в F, положив

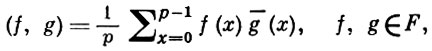
то функции f_a(m), а = 0, 1, ..., р-1, составят ортонормированный базис F. При этом

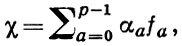
где α_a = 1/p τ_a(χ). Таким образом, Г. с. τ_a(χ) (с точностью до множителя 1/р) являются координатами в разложении мультипликативного характера χ по аддитивным характерам f_a. Возможность линейного представления любого характера χ = χ(m, q) в виде линейной комбинации экспонент

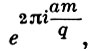
вытекающая из свойств Г. с. общего вида, лежит в основе вывода функционального уравнения для L-функции.

Эти же соображения существенно используются в методе большого решета при переходе от оценок сумм от аддитивных характеров к оценкам сумм от мультипликативных характеров. Г. с. применяются также для представления L-функций в виде конечных сумм. Такое представление используется в задаче о числе классов дивизоров кругового поля.

Вопрос о знаке Г. с. τ_a(χ), принадлежащей квадратичному характеру, может быть поставлен в более общем виде для Г. с., принадлежащей характеру χ порядка k ≥ 3. Так возникает Куммера гипотеза относительно кубических Г. с. по простому модулю р ≡ 1 (mod 3) и обобщения этой гипотезы на случай k > 3.

Лит.: [1] Карл Фридрих Гаусс. Сб. статей, М., 1956; [2] Виноградов И. М., Метод тригонометрических сумм в теории чисел, М., 1971; [3] Дэвенпорт Г., Мультипликативная теория чисел, пер. с англ., М., 1971; [4] Прахар К., Распределение простых чисел, пер. с нем., М., 1967; [5] Xассе Г., Лекции по теории чисел, пер. с нем., М., 1953.

Б. М. Бредихин.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.