ГАУССА КВАДРАТУРНАЯ ФОРМУЛА

ГАУССА КВАДРАТУРНАЯ ФОРМУЛА - квадратурная формула вида

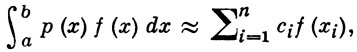
в к-рой узлы x_i и веса с_i подбираются так, чтобы формула была точна для функций

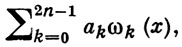
где ω_k(х) - заданные линейно независимые функции (пределы интегрирования могут быть и бесконечными). Г. к. ф. введены К. Гауссом (см. [1]) для а = -1, b = 1, р(х) ≡ 1. Полученная им общая формула, точная для произвольного многочлена степени не выше 2n - 1, имеет вид

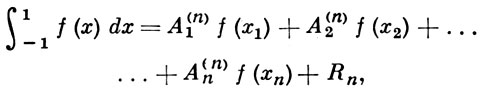
где x_k - корни Лежандра многочлена Р_n(х), а А⁽ⁿ⁾_k и R_n определяются по формулам

Применяется в тех случаях, когда подинтегральная функция достаточно гладкая, а выигрыш в числе узлов крайне существен: напр., если f(x) определяется из дорогостоящих экспериментов, или при вычислении кратных интегралов как повторных. При практическом применении в таких случаях очень важен удачный подбор весовой функции р(х) и функций ω_j(x).

Для широких классов р(х) и ω_j(х) составлены таблицы узлов Г. к. ф. (см. [1]), в частности в [5] при р(х) ≡ 1, ω_j(x) = x^j до n = 512.

При р(х) ≡ 1, ω_j(x) = x^j Г. к. ф. применяется в стандартных программах интегрирования с автоматич. выбором шага как метод вычисления интегралов по подотрезкам разбиения (см. [6]).

Лит.: [1] Gauss С. F., Werke, Bd 3, Gött., 1866, S. 163-196; [2] Кpылов В. И., Приближенное вычисление интегралов, М., 1959; [3] Крылов В. И., Шульгина Л. Т., Справочная книга по численному интегрированию, М., 1966; [4] Бахвалов Н. С., Численные методы, М., 1973; [5] Strоud А. Н., Secrest D., Gaussian Quadrature Formulas, N. Y., 1966; [6] Стандартная программа для вычисления однократных интегралов по квадратурам типа Гаусса, в. 26, М., 1967.

Н. С. Бахвалов, В. П. Моторный.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.