ГАУССА ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА

ГАУССА ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА - формула, использующая в качестве узлов интерполяции ближайшие к точке интерполирования х узлы. Если x = x₀ + th, то формула

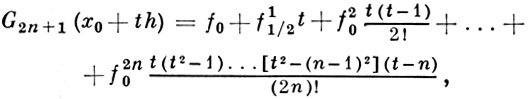
(1)

написанная по узлам x₀, x₀ + h, x₀ - h, ..., x₀ + nh, x₀- nh, наз. формулой Гаусса для интерполирования вперед, а формула

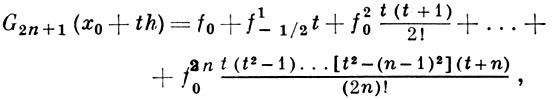
(2)

написанная по узлам x₀, x - h, x₀ + h, ..., x₀ - nh, x₀ + nh, наз. формулой Гаусса для интерполирования назад (см. [1], [2]). В формулах (1) и (2) использованы конечные разности, определяемые следующим образом:

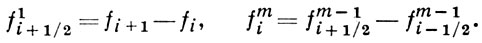
Преимущество Г. и. ф. состоит в том, что указанный выбор узлов интерполяции обеспечивает наилучшую оценку остаточного члена по сравнению с любым другим выбором, а упорядоченность узлов по мере их близости к точке интерполяции уменьшает вычислительную погрешность интерполирования.

Лит.: [1] Березин И. С., Жидков Н. П., Методы вычислений, т. 1, 3 изд., М., 1966; [2] Бахвалов Н. С., Численные методы, М., 1973.

М. Н. Самарин.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.