ГАУССА ЗАКОН ВЗАИМНОСТИ

ГАУССА ЗАКОН ВЗАИМНОСТИ - соотношение, связывающее значения Лежандра символов (p/q) и (q/p) для различных нечетных простых чисел р и q (см. Квадратичный закон взаимности). Кроме основного Г. з. в. для квадратичных вычетов, заключающегося в соотношении:

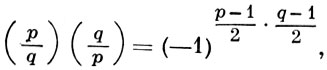
имеются еще два дополнения к указанному закону, а именно:

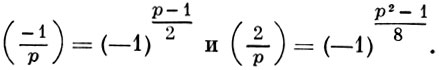
Закон взаимности для квадратичных вычетов был впервые высказан Л. Эйлером (L. Euler, 1772). А. Лежандр (A. Legendre, 1785) дал формулировку закона в современной форме и доказал часть этого закона. Первое полное доказательство Г. з. в. было дано К. Гауссом (С. Gauss, 1801) (см. [1]). В течение жизни К. Гаусс дал восемь различных доказательств квадратичного закона взаимности, построенных на различных принципах.

Попытки установить закон взаимности для кубияее-ких и биквадратичных вычетов привели К. Гаусса к введению кольца целых комплексных чисел.

Лит.: [1] Гаусс К. Ф., Труды по теории чисел, пер. с нем. и латин., М., 1959; [2] Виноградов И. М., Основы теории чисел, 8 изд., М., 1972; [3] Xассе Г., Лекции по теории чисел, пер. с нем., М., 1953.

С. А. Степанов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.