ГАУССА ВАРИАЦИОННАЯ ЗАДАЧА

ГАУССА ВАРИАЦИОННАЯ ЗАДАЧА - вариационная задача, исследованная впервые К. Гауссом [1] и в современных терминах формулируемая следующим образом. Пусть μ - положительная мера в евклидовом пространстве ℝⁿ(n ≥ 3), имеющая конечную энергию (см. Энергия мер), и пусть

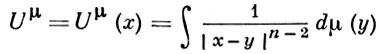
- ньютонов потенциал меры μ. Требуется среди всех мер λ с компактным носителем K ⊂ ℝⁿ найти такую меру μ₀, к-рая дает минимум интегралу

∫(U^λ - 2U^μ)dλ,

представляющему собой скалярное произведение (λ-2μ, λ) в предгильбертовом пространстве мер.

Значение Г. в. з. определяется тем, что равновесная мера (см. Робена задача) может быть получена как решение Г. в. з. при определенном выборе меры μ; напр. можно принять за μ равномерное распределение массы на сфере с центром в начале координат, охватывающей множество K.

Лит.: [1] Gauss С. F., Werke, Bd 5, Gött., 1867, S. 195-242; [2] Ландкоф Н. С., Основы современной теории потенциала, М., 1966, гл. 2; [3] Брело М., Основы классической теории потенциала, пер. с франц., М., 1964, гл. 11.

Е. Д. Соломенцев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.