ГАТО ДИФФЕРЕНЦИАЛ

ГАТО ДИФФЕРЕНЦИАЛ отображения f(x) линейного топологич. пространства X в линейное топологич. пространство Y - функция

h → Df(x₀, h),

где предел

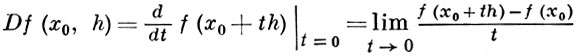
в предположении, что он существует для всех h ∈ Х, а сходимость понимается в топологии пространства Y. Так определенный Г. д. однороден, но неаддитивен. Аналогично вводятся Г. д. высших порядков. Отображение h → Df(х₀, h) наз. иногда Гато вариацией, или слабым дифференциалом (см. также Дифференцирование отображений, Вариация).

Обычно накладывают дополнительное требование линейности и непрерывности. Г. д.: Df(х, h) = f'_Г(x₀)h, f'_Г(х₀) ∈ L(X, Y). В этом случае f'_Г(х₀) наз. Гато производной. Если отображение (х, h) → Df(x, h) равномерно непрерывно по x и непрерывно по h в нек-рой области, то в этой области существует Фреше производная f (х) и при этом f'(х)h = Df(x, h).

Лит.: [1] Люстерник Л. А., Соболев В. И., Элементы функционального анализа, 2 изд., М., 1965; [2] Колмогоров А. Н., Фомин С. В., Элементы теории функции и функционального анализа, 4 изд., М., 1976.

В. М. Тихомиров.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.