ГАТО ГРАДИЕНТ

ГАТО ГРАДИЕНТ функционала f(x) в точке х₀ гильбертова пространства Н - вектор из H, равный Гато производной f'_Г(x₀) функционала f в точке х₀. Иначе говоря, Г. г. определяется формулой

f(x₀ + x) = f(x₀) + (f'_Г(x₀), h) + ε(h),

где ε(th)/t → 0 при t → 0. В n-мерном евклидовом пространстве Г. г. f'_Г(x₀) есть вектор с координатами

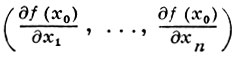
и наз. обычно градиентом. Понятие Г. г. распространяется на случай, когда X - риманово многообразие (конечномерное или гильбертово бесконечномерное), а f - гладкая действительная функция на X. Направление вдоль Г. г. среди всех направлений, проходящих через точку х₀, выделяется наибольшим ростом функции f.

В. М. Тихомиров.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.