ГАТО ВАРИАЦИЯ

ГАТО ВАРИАЦИЯ отображения f(x) линейного пространства X в линейное топологического пространство Y - предел в топологии пространства Y:

(*)

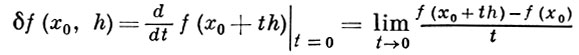
в предположении, что он существует для всех h ∈ X. Именно так ввел первую вариацию Р. Гато (R. Gateaux) в 1913-14. Для функционалов классического вариационного исчисления это определение было дано Ж. Лагранжем (см. Вариация функционала).

Выражение δf(х₀, h) не обязательно является линейным функционалом по h, хотя оно всегда есть однородная функция по h первой степени. Отображение h → δf(х₀, h) называют иногда Гато дuффepeнцuaлoм. Начиная с работ П. Леви ([2], см. также [3]), обычно требуют линейность и непрерывность δf(x₀, h) по h:

δf(x₀, h) = f'_Г(х₀) h, f'_Г(х₀) ∈ L(X, Y).

В этом случае f'_Г(x₀) наз. Гато производной. Аналогично (*) определяются вторая и т. д. вариации. См. также Вариация, Вторая вариация, Дифференцирование отображений.

Лит.: [1] Gateaux R., «С. r. Acad. sci.», 1913, t. 157, p. 325-27; «Bull. soc. math. France», 1919, t. 47, p. 70-96; [2] Levy P., Lecons d'analyse fonctionnelles, P., 1922; [3] Леви П., Конкретные проблемы функционального анализа, пер. с франц., М., 1967.

В. М. Тихомиров.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.