ГАРНАКА ТЕОРЕМА

ГАРНАКА ТЕОРЕМА - 1) Первая Г. т.: если последовательность функций, гармонических в ограниченной области G и непрерывных на G̅, равномерно сходится на границе ∂G, то она равномерно сходится на G к гармонич. функции. Первая Г. т. имеет следующее обобщение для решений эллиптич. уравнения

(*)

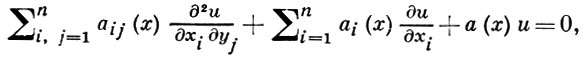
имеющего единственное решение Дирихле задачи при любой непрерывной краевой функции (см. [1]). Если последовательность решений уравнения (*) равномерно сходится на ∂G, то она равномерно сходится на G к решению уравнения (*).

2) Вторая Г. т., принцип Гарнака: если монотонная последовательность функций, гармонических в ограниченной области G, сходится в некоторой точке из G, то она сходится во всех точках области G к гармонич. функции, и эта сходимость равномерна в любой замкнутой подобласти области G. Вторая Г. т. допускает обобщение и для монотонной последовательности решений эллиптич. уравнения (*).

Лит.: [1] Петровский И. Г., Лекции об уравнениях с частными производными, 3 изд., М., 1961; [2] Фридман А., Уравнения с частными производными параболического типа, пер. с англ., М., 1968.

Л. И. Камынин.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.