ГАРНАКА НЕРАВЕНСТВО

ГАРНАКА НЕРАВЕНСТВО (двойное) - неравенство, оценивающее сверху и снизу отношение u(х)/u(у) двух значений положительной гармонич. функции; получено А. Гарнаком (Харнаком) [1]. Пусть u(х) ⊒ 0 -гармоническая в области G n-мерного евклидова пространства функция, Е_r(у) - шар {x : |x - y| < r} радиуса r с центром в точке у. Если замыкание E̅_r(y) ⊂ G, то для всех х ∈ Е_ρ(у), 0 ≤ ρ < r, справедливо неравенство Гарнака

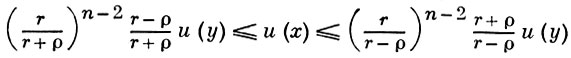
или

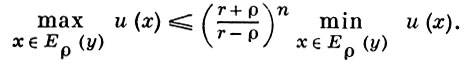
Если g - компакт, g̅ ⊂ G, то существует число M = M(G, g), такое, что

М^-1 u(у) ≤ u(х) ≤ Мu(у) (2)

для любых х, y ∈ g̅. В частности,

Из Г. н. следуют: сильный принцип максимума, Гарнака теоремы о последовательностях гармонич. функций теоремы о компактности семейств гармонич. функций, Лиувилля теорема и другие факты. Г. н. обобщается ([3], [4]) на неотрицательные решения широкого класса линейных эллиптич. уравнений вида

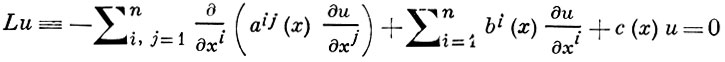
с равномерно положительно определенной матрицей ||a^ij||:

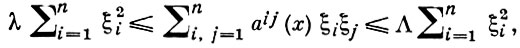
где Λ ≥ λ > 0 - числа, ξ = (ξ₁, ..., ξ_n)- любой n-мерныи вектор, x ∈ G. При этом постоянная М неравенства (2) зависит только от λ, Λ, некоторых норм младших коэффициентов оператора L и расстояния между границами G и g.

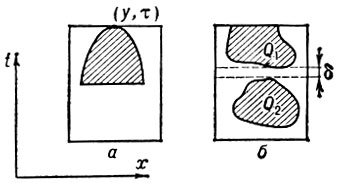
Для неотрицательных решений u(х, t) равномерно параболич. уравнений вида u_t + Lu = 0 (коэффициенты оператора L могут зависеть и от t) аналог Г. н. также имеет место [5]. В этом случае возможно только одностороннее неравенство

u(х, t) ≤ Mu(y, τ)

для точек (х, t), лежащих внутри параболоида

{(x, t):|x - y|² ≤ μ²(τ - t), τ - ν² ≤ t ≤ τ}

с вершиной в точке (у, τ), обращенного полостью вниз (рис. а). При этом М зависит от величин у, τ, λ, Λ, μ, ν, нек-рых норм младших коэффициентов оператора L и от расстояний между границей параболоида и границей области, в к-рой u(x, t) ≥ 0. Если, например, u(х, t) ≥ 0 в цилиндре

Q = G × (a, b], g̅ ⊂ G,

расстояние между ∂G и ∂g больше или равно d > 0 и d достаточно мало, то в g×(a - d², b] выполняется неравенство [5]:

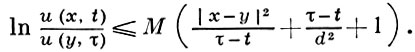
В частности, если u(х, t) ≥ 0 в Q (рис. б) и компакты Q₁, Q₂ вложены в Q, причем

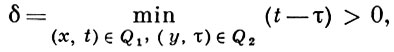
то

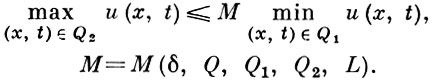
Пример функции

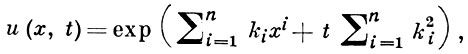
являющейся решением уравнения теплопроводности u_t - Δu = 0 при любых k₁, k₂, ... k_n, показывает невозможность в параболич. случае двусторонних оценок.

Лит.: [1] Наrnасk A., Die Grundlagen der Theorie des logarithmischen Potentiales und die eindeutiger Potentialfunction in der Ebene, Lpz., 1887; [2] Курант P., Уравнения с частными производными, пер. с англ., М., 1964; [3] Серрин Дж., «Математика», 1958, т. 2, № 6, с. 49-62; [4] Моsеr J., «Communs Pure and Appl. Math.», 1961, v. 14, № 3, p. 577-91; [5] его же, там же, 1964, v. 17, № 1, p. 101-34; [6] Фридман А., Уравнения с частными производными параболического типа, пер. с англ., М., 1968; [7] Ландис Е. М., Уравнения второго порядка эллиптического и параболического типов М. 1971.

Л. И. Камынин, Л. П. Купцов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.