ГАРНАКА ИНТЕГРАЛ

ГАРНАКА ИНТЕГРАЛ - обобщение несобственного интеграла Римана на класс функций f, множество точек неограниченности к-рых Е_f имеет нулевую жорданову меру и к-рые интегрируемы по Риману во всяком сегменте, не содержащем точек из Е_f. Пусть Δ_i, i = 1, 2, ..., n,- конечная система интервалов, содержащая Е_f. Тогда Г. и. определяется равенством

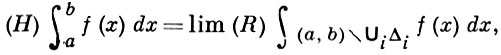
если последний предел при mes ∪_iΔ_i → 0 существует. Г. и. введен А. Гарнаком (Харнаком) [1]. Позднее к этому определению было добавлено требование, чтобы каждый интервал Δ_i имел непустое пересечение с Е_f. При этом Г. и. становится, вообще говоря, условно сходящимся. Г. и. частично перекрывается с Лебега интегралом и покрывается Перрона интегралом и Данжуа интегралом. В настоящее время Г. и. представляет лишь методич. и историч. интерес.

Лит.: [1] Наrnасk A., «Math. Ann.», 1883, Bd 21, S. 305-26; [2] Пeсин И. Н., Развитие понятия интеграла, М., 1966.

В. А. Скворцов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.