ГАРМОНИЧЕСКОЕ ПРОСТРАНСТВО

ГАРМОНИЧЕСКОЕ ПРОСТРАНСТВО - топологич. пространство X с пучком ℌ непрерывных действительных функций с аксиоматически фиксируемыми в той или иной форме тремя основными свойствами классических гармонических функций: свойство сходимости, выражаемое второй Гарнака теоремой; принцип экстремума; разрешимость Дирихле задачи для достаточно широкого класса открытых множеств из X. Функции пучка ℌ получают наименование гармонич. функций; преимущество этого аксиоматич. подхода состоит в том, что с его помощью в теорию включаются решения не только Лапласа уравнения, но и нек-рых других уравнений эллиптич. и параболич. типов. Пусть X - локально компактное топологич. пространство. Под пучком функций на X здесь понимается отображение 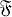, определенное на семействе всех открытых множеств U, V, ... из X и такое, что: 1) 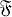(U) есть семейство функций на U; 2) если U ⊂ V, то сужение любой функции из 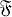(V) на U принадлежит 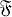(Р); 3) для любого семейства {U_i}_i∈I функция на ∪_i∈IU_i принадлежит 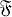(∪_i∈IU), если для всех i ∈ I ее сужение на U_i принадлежит 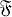(∪_i∈IU_i). Пучок функций 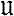наз. гипергармоническим, если 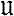(U) для любого U есть выпуклый конус полунепрерывных и конечных снизу действительных функций на U. Пучок функций ℌ наз. гармоническим, если ℌ(U) для любого U есть действительное векторное пространство непрерывных функций на U; в дальнейшем используется только гармонич. пучок

ℌ : U → 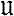(U) ∩ (-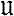(U)).

Локально компактное пространство X наз. Г. п., если выполняются следующие аксиомы (см. [3]).

Аксиома положительности: пучок ℌ невырожден во всех точках х ∈ Х, т. е. для любого х ∈ Х существует функция u ∈ ℌ, определенная в окрестности х, причем u(х) ≠ 0.

Аксиома сходимости: если возрастающая последовательность функций из ℌ(U) локально ограничена, то она сходится к функции из ℌ(U).

Аксиома разрешимости: существует базис разрешимых открытых множеств U, т. е. таких, что для любой непрерывной функции f с компактным носителем на ∂U существует обобщенное в смысле Винера-Перрона (см. Перрона метод) решение задачи Дирихле для U из ℌ(U).

Аксиома мажоранты: если полунепрерывная и конечная снизу функция u на U для любого относительно компактного множества V такого, что V̅ ⊂ U, удовлетворяет условию

sup {v ∈ ℌ(U); v(x) ≤ u(x), x ∈ ∂V} = μ^Vu ≤ u

на V, то 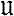u ∈ (U).

Евклидово пространство ℝⁿ, n ≥ 2, с пучком классич. решений уравнения Лапласа или теплопроводности уравнения образует Г. п. Имеется ряд других вариантов аксиоматики гармонич. пространств. Г. п. локально связны, не содержат изолированных точек; они имеют базис из связных разрешимых множеств.

Гипергармонич. функция u на Г. п. X наз. супергармонической, если для любого относительно компактного разрешимого множества V наибольшая миноранта μ^Vu есть гармонич. функция. Положительная супергармонич. функция, для к-рой любая гармонич. миноранта тождественно равна нулю, наз. потенциалом. Г. п. X наз. 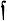-гармоническим (или 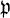-гармоническим), если для любого х ∈ Х существует положительная супергармонич. функция и (или, соответственно, потенциал u) на X такая, что u(x) > 0.

Любое Г. п. допускает покрытие такими открытыми множествами U, для к-рых выполняется принцип минимума в следующей форме: если гипергармоническая функция u ∈ 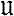(U) положительна вне пересечения U с любым компактом из X и

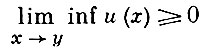
для всех y ∈ ∂U, то u ≥ 0. В случае 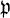-гармонич. пространства этот принцип минимума выполняется для всех открытых множеств. Евклидово пространство ℝⁿ с пучком классич. решений уравнения Лапласа при n ≥ 2 образует 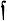-гармонич. пространство, а при n ≥ 3 оно образует 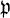-гармонич. пространство; пространство ℝⁿ × ℝ¹, n ≥ 1, с пучком решений уравнения теплопроводности образует 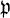-гармонич. пространство.

Основными вопросами теории Г. п. являются: теория разрешимости задачи Дирихле, включающая исследование поведения обобщенного решения этой задачи в граничных точках; теория емкости множеств в Г. п.; изучение проблемы выметания (см. Выметания метод) и Робена задачи.

Лит.: [1] Вrеlоt М., Lectures on potential theory, Bombay, 1960; [2] Bauer H., Harraonische Raume und ihre Potentialtheorie, В., 1966 (Lecture Notes in Mathematics, № 22); [3] Gonstantinescu C., Cornea A., Potential theory on harmonic spaces, В., 1972; [4] Брело M., О топологиях и границах в теории потенциала, пер. с англ., М., 1974.

Е. Д. Соломенцев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.