ГАРМОНИЧЕСКОГО БАЛАНСА МЕТОД

ГАРМОНИЧЕСКОГО БАЛАНСА МЕТОД - приближенный метод исследования нелинейных колебательных систем, описываемых нелинейными обыкновенными дифференциальными уравнениями. Суть Г. б. м. состоит в замене в колебательных системах нелинейных сил специальным образом построенными линейными функциями, в силу чего он позволяет использовать теорию линейных дифференциальных уравнений для приближенного анализа нелинейных систем.

Линейные функции строятся с помощью специального приема, наз. гармонич. линеаризацией. Пусть задана нелинейная функция (сила)

F(х, ẋ) ≡ εf(х, ẋ), ẋ = dx/dt,

где ε - малый параметр. Гармонической линеаризацией наз. замена F(x, ẋ) линейной функцией

F_l(х, ẋ) = kх + λẋ,

где параметры k и λ вычисляются по формулам:

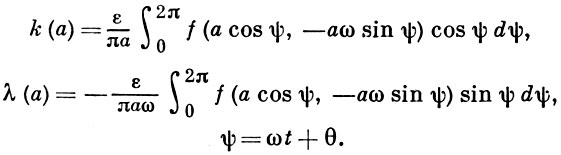
Если x = a cos(ωt + θ), a = const, ω = const, θ = const, то нелинейная сила F(x, ẋ) является периодич. функцией времени, и ее разложение в ряд Фурье содержит, вообще говоря, бесконечное число гармоник с частотами nω, n = 1, 2, ..., т. е. оно имеет вид:

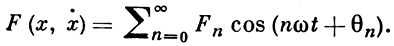
(1)

Слагаемое F₁cos(ωt + θ₁) наз. основной гармоникой разложения (1). Амплитуда и фаза линейной функции F_l совпадают с аналогичными характеристиками основной гармоники нелинейной силы.

Применительно к дифференциальному уравнению

ẍ + ω²x + F(x, ẋ) = 0, (2)

типичному для теории квазилинейных колебаний, Г. б. м. заключается в замене F(x, ẋ) линейной функцией F_l, и вместо уравнения (2) рассматривается уравнение

ẍ + λẋ + k₁x = 0, (3)

где k₁ = ω² + k. Принято называть F_l эквивалентной линейной силой, λ - эквивалентным коэффициентом затухания, k₁ - эквивалентным коэффициентом упругости. Доказано, что если нелинейное уравнение (2) имеет решение вида

х = а cos(ωt + θ),

причем

ȧ = O(ε), ω = O(ε),

то разность между решениями уравнений (2) и (3) имеет порядок ε². В Г. б. м. частота колебаний зависит от амплитуды а (посредством величин k и λ).

Г. б. м. применяется для отыскания периодич. и квазипериодич. колебаний, периодич. и квазипериодич. режимов в теории автоматич. регулирования, стационарных режимов и для исследования их устойчивости. Особенно большое распространение он получил в теории автоматич. регулирования.

Лит.: [1] Крылов Н. М., Боголюбов Н. Н., Введение в нелинейную механику, К., 1937; [2] Боголюбов Н. Н., Митропольский Ю. А., Асимптотические методы в теории нелинейных колебаний, 4 изд., М., 1974; [3] Попов Е. П., Пальтов И. П., Приближенные методы исследования нелинейных автоматических систем, М., 1960.

Е. А. Гребеников.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.