
ГАРМОНИЧЕСКИЙ АНАЛИЗ АБСТРАКТНЫЙ
ГАРМОНИЧЕСКИЙ АНАЛИЗ АБСТРАКТНЫЙ - теория абстрактных Фурье рядов и Фурье интегралов. Классический гармонич. анализ - теория рядов Фурье и интегралов Фурье - интенсивно развивался под влиянием физич. задач в 18-19 вв., и в работах П. Дирихле (P. Dirichlet), Б. Римана (В. Biemann), А. Лебега (Н. Lebesgue), М. Планшереля (М. Plancherel), Л. Фейера (L. Fejér), Ф. Рисса (F. Biesz) оформился в самостоятельную математич. дисциплину.
Дальнейшее развитие гармонич. анализа привело к установлению разнообразных связей гармонич. анализа с общими вопросами теории функций и функциональным анализом. Открытие Хаара меры и развитие теории представлений бесконечных групп, начиная с работ Г. Вейля и Ф. Петера (см. [1]) по теории представлений бикомпактных групп и работ Л. С. Понтрягина [2] по теории характеров локально бикомпактных абелевых групп, поставили вопрос о естественных границах основных результатов классического гармонического анализа. Эта задача основана на следующей интерпретации обычного ряда Фурье в комплексной форме. Пусть f(x)- комплекснозначная суммируемая с квадратом функция на окружности единичной длины (или на отрезке [0, 1]), сn - ее коэффициенты Фурье по системе {e2πinx, n - целое}:
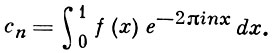
Тогда ряд Фурье
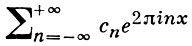
функции f(x) сходится в среднем к f(х) в L2[0, 1]. Мера Лебега на [0, 1] порождает меру Хаара на окружности (единичной длины) G, рассматриваемой как группа вращений плоскости, а функции x → e2πinx представляют собой полный набор неприводимых унитарных представлений топологич. группы G. Поэтому все величины, входящие в определение ряда Фурье, получают теоретико-групповой смысл и появляется возможность обобщения понятия ряда Фурье, основанная на теории неприводимых унитарных представлений топология, групп. При этом Г. а. а. не только позволяет найти естественную форму результатов классического гармонич. анализа на прямой или окружности, но и установить новые результаты, относящиеся к большим классам топологич. групп.
Г. а. а. как гармонический анализ на группах зародился в значительной мере на основе теории характеров локально бикомпактных абелевых групп, созданной Л. С. Понтрягиным [2] (см. также [7], [8], [9]). Г. а. а. является одной из естественных областей приложения методов теории банаховых алгебр и может до нек-рой степени рассматриваться как одна из ветвей этой теории. С другой стороны, рамки Г. а. а. являются естественными для ряда классических задач теории функций и функционального анализа.
Приложения Г. а. а. весьма многообразны. Результаты Г. а. а. применяются в общей теории локально бикомпактных групп (напр., в структурных теоремах), в теории динамич. систем, в теории представлений бесконечных групп (к-рая, в свою очередь, служит одним из основных инструментов Г. а. а.) и во многих других математич. теориях.
Наиболее разработанным разделом Г. а. а. является теория интеграла Фурье на локально бикомпактной абелевой группе. Среди некоммутативных групп особое положение занимают бикомпактные группы, теория представлений к-рых имеет сравнительно простой и законченный вид: для бикомпактных групп получен ответ на многие классич. вопросы гармонич. анализа. В случае небикомпактных некоммутативных групп общая теория далека от завершения (1977). Однако и в этом случае известны естественные границы ряда фундаментальных результатов классического гармонич. анализа.
Связь задач Г. а. а. с теорией банаховых алгебр основана на возможности построить по любой локально бикомпактной топологич. группе G две банаховы алгебры, играющие большую роль в теории представлений группы G: групповую алгебру и алгебру мер М(G), к-рая определяется следующим образом. Пусть С0(G)-множество непрерывных функций f на G с бикомпактным носителем, M(G) - банахово пространство ограниченных регулярных мер на G. Введение в М(G) умножения - свертки (μ1, μ2) → μ1 * μ2 и инволюции μ → μ* посредством соотношений (для всех f ∈ С0)
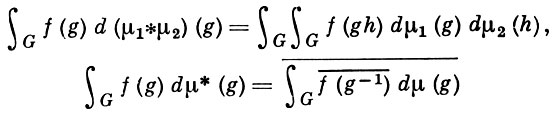
превращает M{G) в банахову алгебру с инволюцией, называемую алгеброй мер группы G. Если dg - левоинвариантная мера Хаара на G, то сопоставление каждому элементу f(g) групповой алгебры L1(G) меры f(g)dg приводит к изометрич. отображению алгебры L1(G) на замкнутую подалгебру алгебры мер M(G), сохраняющему инволюцию. В этом смысле L1(G) может рассматриваться как замкнутая подалгебра алгебры M(G).
Г. а. а. на локально бикомпактной абелевой группе. Для построения интеграла Фурье на локально бикомпактной абелевой группе G необходимы следующие факты. Любое неприводимое унитарное представление G одномерно и определяет непрерывный гомоморфизм G в мультипликативную группу U комплексных чисел с модулем 1. Такое отображение χ: G → U наз. унитарным характером группы G. Пусть Ĝ - группа характеров группы G. Теорема двойственности Понтрягина утверждает, что отображение η: G → Ĝ, определяемое формулой
(η(g)) (χ) = χ(g),
где χ ∈ Ĝ, g ∈ G, есть топологич. изоморфизм группы G на Ĝ (см. [2], [3], [4], [6]). При этом группа G бикомпактна тогда и только тогда, когда двойственная к ней группа Ĝ дискретна. Группа характеров аддитивной группы К недискретного локально бикомпактного поля изоморфна K; группа характеров группы U изоморфна группе целых чисел Z. Если Н - замкнутая подгруппа группы G и Н⊥ - множество таких χ ∈ G, что χ ≡ 1 на Н, то Н⊥ есть замкнутая подгруппа группы G, (H⊥)⊥ = η(H), Ĝ/H⊥ ≈ Ĥ, и любой унитарный характер подгруппы Н продолжается до унитарного характера группы G.
Интегралом Фурье на группе G (или преобразованием Фурье на группе G) наз. отображение F, к-рое мере μ ∈ M(G) ставит в соответствие функцию μ̂ = Fμ на Gμ, определяемую равенством
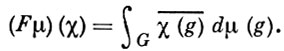
Копреобразованием Фурье наз. отображение F̅, определяемое равенством
(F̅μ)(σ) = ∫G χ(g)dμ(g), μ ∈ M(G).
Для f ∈ L1(G) функция F(f(g)dg) обозначается f̂ или Ff (соответственно F̅f). Отображения F и F̅ являются мономорфизмами M(G) в L∞(Ĝ); образом для М(G) при этих отображениях служит алгебра В(G) линейных комбинаций непрерывных положительно определенных функций на G. Справедлива обобщенная теорема Бохнера (см. [4], [6]): функция Fμ является положительно определенной функцией на G тогда и только тогда, когда μ - положительная мера, и в этом случае
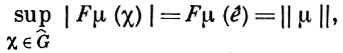
где ê - единица группы Ĝ.
Топологич. пространство Ĝ канонически гомеоморфно спектру кольца L1(G) (или пространству максимальных идеалов алгебры L1(G)). Именно, характеру χ ∈ Ĝ ставится в соответствие характер коммутативной алгебры L1(G), определяемый формулой
f → ∫G f(g)χ(g)dg, f ∈ L1(G);
при этом копреобразование Фурье F̅ совпадает на L1(G) с Гельфанда представлением алгебры L1(G). Спектр кольца M(G), вообще говоря, не гомеоморфен Ĝ.
Пусть dχ - мера Хаара на Ĝ, a L2(Ĝ)- соответствующее гильбертово пространство. Справедлива следующая теорема Планшереля (см. [4], [16]): если f ∈ L1(G) ∩ L2(G), то Ff ∈ L2(Ĝ), и при нек-рой нормировке мер dg и dχ отображение f → Ff множества L1(G) ∩ L2(G) в L2(Ĝ) продолжается единственным образом до унитарного оператора F из L2(G) в L2(Ĝ). Этот оператор наз. преобразованием Фурье в L2(G). В этом случае меры dg и dχ наз. согласованными. Пусть через A(G) обозначено линейное подпространство пространства порожденное функциями вида f*g, где f, g ∈ L1(G) ∩ L2(G). Справедлива следующая формула обращения Фурье (см. [4], [16]): если f ∈ A(G), то Ff ∈ L1(Ĝ) и для всех g ∈ G имеет место равенство
f(g) = ∫Ĝ χ(g) (Ff) (χ) dχ,
т. е. если η - каноническое отображение G в Ĝ, то f = (F̅Ff) ○ η для всех f ∈ A(G). Пусть ℬ(G)- множество таких f ∈ L1(G), что f ∈ L1(G). Тогда сужение F на ℬ(G) есть взаимно однозначное отображение ℬ(G) на ℬ(Ĝ); обратное отображение есть сужение F̅ на ℬ(Ĝ). Если f, g ∈ L2(G), то F(fg)= (Ff)*(Fg).
Классическая Пуассона формула суммирования получает в Г. а. а. следующую естественную интерпретацию. Пусть Н - замкнутая подгруппа группы G, dg - мера Хаара на G, dh - мера Хаара на Н и dk - мера Хаара на K = G/H. Пусть (G/H)^ отождествляется с H⊥ и dρ - мера Хаара на H⊥, согласованная с dk. Наконец, пусть f ∈ L1(G) и пусть сужение на H⊥ непрерывной функции Ff интегрируемо по мере dρ. Тогда для почти всех g ∈ G функция h → f(gh) на H интегрируема по мере dh, и
∫H f(gh) dh = ∫H⊥ ρ(g) (Ff) (ρ) dρ.
Эта формула наз. обобщенной формулой суммирования Пуассона.
Важной внутренней задачей Г. а. а. является изучение банаховых алгебр L1(G) и М(G) с точки зрения преобразования Фурье на G. Алгебра L1(G) есть вполне симметричная алгебра. Равенство М(G) = L1(G) имеет место тогда и только тогда, когда G дискретна. Если G не дискретна, то М(G) содержит несимметричные максимальные идеалы. Пусть A(Ĝ) (соответственно B(Ĝ)) - множество преобразований Фурье элементов алгебры L1(G) (соответственно M(G)). A(Ĝ) и B(Ĝ) являются алгебрами функций на Ĝ; при этом A(Ĝ) - регулярная алгебра, и f ∈ A(Ĝ) тогда и только тогда, когда f = f1 * f2 для нек-рых f1, f2 ∈ L2(Ĝ). Множество тех f ∈ L1(G), для к-рых носитель функции Ff бикомпактен, есть плотное подмножество в L1(G).
Следующие результаты описывают функциональные свойства преобразования Фурье на G. Пусть F -функция, определенная на [-1, 1], и пусть Ĝ недискретна. Пусть F действует на A(Ĝ), т. е. F(φ) ∈ A(Ĝ) для любой функции φ ∈ A(G), область значений к-рой лежит в [-1, 1]. Тогда F аналитична на [-1, 1], и если G недискретна, то F(0) = 0. Обратно, аналитическая на [-1, 1] функция F(F(0) = 0, если G недискретна) действует на A(Ĝ). Функция F действует на В(G) тогда и только тогда, когда F есть сужение на [-1, 1] целой вещественной аналитич. функции. Пусть F определена на [-1, 1] и G есть бесконечная дискретная группа. F действует на A(Ĝ) тогда и только тогда, когда F(0) = 0 и F аналитична в некоторой окрестности начала (см. [12], [13], где имеется подробная библиография).
Традиционным вопросом теории банаховых алгебр является вопрос о структуре и свойствах замкнутых подалгебр. Следующие результаты относятся к замкнутым подалгебрам алгебры L1(G). Пусть S - борелевская полугруппа в локально бикомпактной абелевой группе G и L1(S) - максимальная подалгебра в L1(G). Тогда S содержится в замкнутой полугруппе P ⊂ G, индуцирующей архимедов порядок на G. Коммутативная банахова алгебра А наз. алгеброй Стоуна-Вейерштрасса, если любая ее симметричная подалгебра В ⊂ А, отделяющая точки спектра М кольца A и не обращающаяся в нуль одновременно ни в одной точке из М, плотна в А. L1(G) есть алгебра Стоуна-Вейерштрасса в том и только в том случае, если G вполне несвязна.
Одним из направлений современных исследований в Г. а. а. является теория тонких множеств в локально бикомпактных абелевых группах, к-рая может рассматриваться как обобщение более специальных результатов классического гармонич. анализа (в частности, теории лакунарных тригонометрич. рядов). Пусть G - локально бикомпактная абелева группа, е - единица группы G. Множество E ⊂ G наз. независимым, если для любых g1, ..., gk ∈ Е и целых n1, ..., nk либо g1n1 = g2n2 = ... = gknk = e, либо Пki=1 gini ≠ e. Любая недискретная локально бикомпактная абелева группа содержит независимое множество, гомеоморфное канторову множеству. Среди независимых множеств следует выделить два важных класса множеств, а именно, множества Кронекера и множества типа Кq в группах Dq. Множество Е в локально бикомпактной абелевой группе наз. множеством Кронекера, если для любой непрерывной функции f на Е с модулем 1 и для любого ε > 0 существует такой характер χ ∈ Ĝ, что sup/E |f(g) - χ(g)| < ε. Множество Кронекера независимо и не содержит элементов конечного порядка. Пусть ℤq -циклич. группа порядка q ≥ 2 и Dq - прямое произведение счетного числа групп, изоморфных ℤq. Множество Е в Dq наз. множеством типа Kq, если любая непрерывная функция f: Е → ℤq (ℤq рассматривается как группа корней из единицы) совпадает на E с нек-рым унитарным характером группы Dq. Множества типа Кq независимы. Если в любой окрестности единичного элемента локально бикомпактной группы G содержится элемент бесконечного порядка, то G содержит множество Кронекера, гомеоморфное канторову множеству. Если G - недискретная локально бикомпактная абелева группа и если существует окрестность единичного элемента без элементов бесконечного порядка, то G содержит Dq (для нек-рого q ≥ 2) как замкнутую подгруппу; любая группа Dq содержит множество типа Kq, гомеоморфное канторову множеству.
В конечномерных метрических локально бикомпактных абелевых группах независимое множество есть вполне несвязное множество. Бесконечномерный тор содержит множество Кронекера, гомеоморфное отрезку. Объединение двух множеств Кронекера на окружности может оказаться независимым множеством, не являющимся множеством Кронекера. На бесконечномерном торе добавлением одной точки к нек-рому множеству Кронекера можно получить независимое множество, не являющееся множеством Кронекера. Если Е - бикомпактное множество Кронекера в G и μ - ограниченная мера, сосредоточенная на Е, то
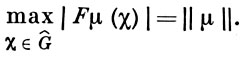
Другой важный класс подмножеств локально бикомпактных абелевых групп образуют множества Хельсона - бикомпактные множества P ⊂ G, обладающие тем свойством, что любая непрерывная функция F на Р есть сужение на Р нек-рого элемента алгебры A(Ĝ). Всякое бикомпактное множество Кронекера и всякое бикомпактное множество типа Kq в Dq являются множествами Хельсона. Не всякое счетное бикомпактное подмножество локально бикомпактной абелевой группы G есть множество Хельсона; существуют независимые канторовы множества, не являющиеся таковыми. Бикомпактное подмножество P ⊂ G будет множеством Хельсона тогда и только тогда, когда ||μ|| и supĜ|F(μ)(χ)| эквивалентные нормы на банаховом пространстве М(Р) ограниченных мер на Р. Пусть через I(Р) обозначено множество всех тех f ∈ L1(G), для которых (F̅f)(g) = 0 при всех g ∈ P. Тогда I(Р) есть замкнутый идеал в L1(Ĝ). Сопряженное пространство к L1(Ĝ)/I(Р) изометрично пространству Ф(Р), состоящему из всех тех φ ∈ L∞(Ĝ), для к-рых
∫Ĝ f(χ) φ(χ-1) dχ = 0
при любых f ∈ I(Р). Бикомпактное множество Р является множеством Хельсона тогда и только тогда, когда любая функция φ ∈ Ф(Р) равна почти всюду преобразованию Фурье нек-рой ограниченной меры, сосредоточенной на Р. Если Р - множество Хельсона в G и σ -ненулевая мера, сосредоточенная на Р, то Fσ не стремится к нулю на бесконечности.
При изучении рядов Фурье на бикомпактных абелевых группах большую роль играет понятие множеств Сидона в дискретных абелевых группах. Пусть G - бикомпактная абелева группа, Е - подмножество G. Функция f ∈ L1(G) наз. Е-функцией, если f̂(χ) = 0 для всех χ ∈ Е. Линейная комбинация f унитарных характеров на G наз. Е-многочленом, если f есть E-функция. Множество Е наз. множеством Сидона, если существует такая постоянная В = ВE, что
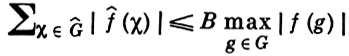
для любого E-многочлена на G. Следующие условия эквивалентны:
Е есть множество Сидона в Ĝ;
для любой ограниченной E-функции f ряд
∑χ∈Ĝ |f̂(χ)|
сходится;
для любой непрерывной E-функции f ряд
∑χ∈Ĝ |f̂(χ)|
сходится;
любая ограниченная функция f на Е совпадает с сужением на Е нек-рого элемента f̂ ∈ B(G);
любая функция на Е, стремящаяся к нулю на бесконечности, совпадает с сужением на Е нек-рой функции f̂ &# 8712; A(G).
Любое бесконечное множество в Ĝ содержит бесконечное множество Сидона. Любое независимое подмножество из Ĝ есть множество Сидона.
Другим интенсивно развивающимся направлением Г. а. а., тесно связанным с теорией тонких множеств, является теория замкнутых идеалов в L1(G), и в частности теория спектрального синтеза. Общая постановка задачи спектрального синтеза такова. Пусть I есть замкнутый идеал в L1(G); требуется выяснить, при каких условиях I является пересечением максимальных идеалов в L1(G), содержащих I (при этом следует отметить, что любой максимальный идеал в L1(G) регулярен, т. е. замкнут). Одним из важнейших результатов теории спектрального синтеза - Винера тауберова теорема: если J - замкнутый идеал в L1(G), J ≠ L1(G), то существует такой характер χ ∈ Ĝ, что (Ff) (χ) = 0 для всех f ∈ J. Это утверждение может рассматриваться как положительное решение поставленной выше проблемы для случая I = L1(G). Если любой замкнутый идеал в L1(G) есть пересечение содержащих его максимальных идеалов, то говорят, что G допускает спектральный синтез. Бикомпактная группа допускает спектральный синтез. С другой стороны, справедлива теорема [15]: если группа Ĝ недискретна, то G не допускает спектрального синтеза. Отсюда следует, что если Ĝ недискретна, то алгебра L1(G) имеет несимметричные замкнутые идеалы.
Г. а. а. на бикомпактных группах может рассматриваться как часть теории представлений бикомпактных групп; эта теория тесно связана с теорией почти периодич. функций на группах; см. также Бора компакт и обзоры в [11], [4]. Задачи Г. а. а. на произвольной локально бикомпактной топологич. группе значительно сложнее ввиду недостаточной разработанности и сложности общей теории бесконечномерных представлений локально бикомпактной группы. Однако и в этом случае можно определить интеграл Фурье на локально бикомпактной группе (см. [5]) и получить аналог обобщенной теоремы Бохнера, формулу Планшереля и ряд других общих теорем (см. [8], [11]).
Лит.: [1] Реter F., Wеуll Н., «Маth. Аnn.», 1927, Bd 97, S. 737-55; [2] Понтрягин Л. С., «Аnn. Math.», 1934, v. 35, p. 361-88; [3] Kampen Е. R. van, «Рrос. Nat. Acad. Sci. USA», 1934, v. 20, p. 434-36; [4] Вeйль А., Интегрирование в топологических группах и его применения, пер. с франц., М., 1950; [5] Гельфанд И. М., Райков Д. А., «Матем. сб.», 1943 т 13, с. 301-16; [6] Райков Д. А., «Тр. Матем. ин-та АН СССР», 1945, т. 14, с. 1-86; [7] Гельфанд И. М., Райков Д. А., Шилов Г. Е., Коммутативные нормированные кольца, М., 1960; [8] Наймарк М. А., Нормированные кольца, 2 изд М., 1968; [9] Понтрягин Л. С., Непрерывные группы, 2 изд., М., 1954; [10] Бурбаки Н., Спектральная теория, пер. с франц., М., 1972; [11] Диксмье Ж., С*-алгебры и их представления, пер. с франц., М., 1974; [12] Нelson Н., (а. о.), «Acta Math.», 1959, v. 102, p. 135-57; [13] Хьюитт Э., Росс К., Абстрактный гармонический анализ, пер. с англ., т. 1-2, М., 1975; [14] Люмис Л. X., Введение в абстрактный гармонический анализ, пер. с англ., М., 1956; [15] Malliavin P., «Publ. Math. IHES», 1959, № 2, p. 61-68; [16] Крейн М. Г., «Докл. АН СССР», 1941, т. 30, с. 482-86.
Е. А. Горин, А. И. Штерн.
Источники:
- Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'