ГАРМОНИЧЕСКАЯ ФОРМА

ГАРМОНИЧЕСКАЯ ФОРМА - внешняя дифференциальная форма α на римановом многообразии М, удовлетворяющая уравнению Δǯ = 0, где Δ = dδ + δd - Лапласа оператор, соответствующий римановой метрике на М, а δ - оператор, сопряженный к внешнему дифференциалу d. Если α имеет компактный носитель, то гармоничность формы α равносильна равенствам dα = = δα = 0. Г. ф. степени р на М образуют векторное пространство H^p(М) над полем ℝ. Если риманово многообразие М компактно, то Н^p(М) конечномерно, как ядро эллиптич. оператора Δ. Поскольку Г. ф. замкнута, в силу теоремы де Рама возникает естественное отображение пространства H^p(M) в пространство Н^p(М, ℝ) вещественных когомологий степени р многообразия М. Из Ходжа теоремы следует, что это отображение является изоморфизмом. В частности, гармонич. функции, то есть Г. ф. степени 0, на связном компактном многообразии постоянны.

Г. ф. на компактном римановом многообразии инвариантны относительно любой связной группы изометрий этого многообразия, а для симметрического пространства М пространство H^p(М) совпадает с пространством р-форм, инвариантных относительно наибольшей связной группы изометрий.

Параллельная теория Г. ф. существует для эрмитовых многообразий М. Г. ф. на эрмитовом многообразии М -это комплексная форма, лежащая в ядре оператора Бельтрами-Лапласа □. Г. ф. типа (р, q) составляют пространство H^p,q(М) над ℂ. Если М компактно, то Н^p,q(M) конечномерно и естественно изоморфно пространству когомологий Дольбо. В случае, когда M - кэлерово многообразие, эти два понятия Г. ф. фактически совпадают, поскольку □ = □̄ = 1/2 Δ. В этом случае

H^p,q(M) = H̄^q,p(М)

и

H^k(M) ⊗ ℂ = ∑_p+q=kH^p,q(M).

Пусть ω - кэлерова форма на М, L - оператор внешнего умножения на ω, Λ - сопряженный к L оператор, Н^p,q₀(М) - пространство примитивных гармонических форм типа (р, q), т. е. форм α ∈ H^p,q(М), для которых Λα = 0. Для p ≥ q и p + q ≤ dim_ℂМ справедливо равенство

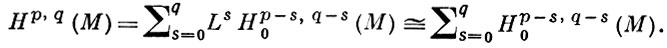
Для компактного кэлерова многообразия M пространство H^p,0(M) совпадает с пространством Ω^p(М) голоморфных форм степени р. В частности,

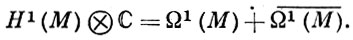
Изучение гармонич. функций и форм на римановых поверхностях восходит к Б. Риману (В. Riemann), сформулированные к-рым теоремы существования были полностью обоснованы к началу 20 в. Теория Г. ф. на компактных римановых многообразиях была впервые изложена У. Ходжем (см. [1]).

В дальнейшем были даны различные обобщения теории Г.ф. Пусть на римановом (соответственно эрмитовом) многообразии М задано локально плоское (соответственно аналитическое) векторное расслоение Е и пусть на слоях расслоения Е задана евклидова (соответственно эрмитова) метрика. При помощи надлежащего обобщения оператора Лапласа (соответственно Бельтрами-Лапласа) (см. [4], [8]) определяются пространства Н^p(Е) (соответственно Н^p,q(Е)) гармонич. форм со значениями в Е (см. Дифференциальная форма). Если М компактно, то эти пространства конечномерны и изоморфны соответствующим пространствам когомологий де Рама и Дольбо, допускающим в свою очередь интерпретацию в терминах когомологий пучков. В случае локально плоского расслоения эти когомологий тесно связаны также с когомологиями группы π₁(М). Если М не компактно, то пространство Г. ф. с интегрируемым квадратом изоморфно пространству когомологий комплекса форм с интегрируемым квадратом [2]. В случае, когда М - область с гладкой границей и компактным замыканием М̅ в кэлеровом многообразии М̃, можно рассматривать также пространство Г. ф. типа (р, q) со значениями в векторном аналитич. расслоении Е над М̃, гладких в М и непрерывных в М̅. Если М строго псевдовыпукла, то это пространство конечномерно и изоморфно пространству когомологий Дольбо, соответствующему Е над М [9].

Г. ф. являются мощным средством изучения когомологий вещественных и комплексных многообразий, а также когомологий дискретных групп. Из теории Г. ф. выводятся основные когомологич. свойства компактных кэлеровых многообразий и, в частности, проективных алгебраич. многообразий [1], [4], [5]. С помощью Г.ф. удается установить связь между кривизной компактного риманова многообразия и тривиальностью некоторых его групп когомологий [6], [7]. Аналогичные связи имеют место в комплексной аналитич. геометрии (см. [4], [5]) и в теории дискретных групп преобразований (см. [8]).

Лит.: [1] Hodge W. V. D., The theory and applications of harmonic integrals, 2 ed., Camb., 1952; [2] де Рам Ж., Дифференцируемые многообразия, пер. с франц., М., 1956; [3] Шварц Л., Комплексные аналитические многообразия. Эллиптические уравнения с частными производными, пер. с исп., М., 1964; [4] Уэллс Р., Дифференциальное исчисление на комплексных многообразиях, пер. с англ., М., 1976; [5] Чжэнь Шэн-шэнь, Комплексные многообразия, пер. с англ., М., 1961; [6] Goldberg S., Curvature and homology, N. Y.-L., 1962; [7] Яно К., Бохнер С., Кривизна и числа Бетти, пер. с англ., М., 1957; [8] Мацусима Й., Мураками С., «Математика», 1965, 9 : 5, с. 27-77; [9] Кон Дж. Дж., «Математика», 1964, 8 : 1, с. 108-41; 8 : 3, с. 80-101.

А. Л. Онищик.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.