ГАРМОНИЗУЕМЫЙ СЛУЧАЙНЫЙ ПРОЦЕСС

ГАРМОНИЗУЕМЫЙ СЛУЧАЙНЫЙ ПРОЦЕСС - комплекснозначная случайная функция X = X(t) действительного параметра t, допускающая представление в виде стохастического интеграла

(*)

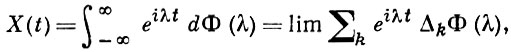
где Ф(λ), -∞ < λ < ∞,- случайный процесс. Приращения Δ_k Ф(λ) = Ф(λ_k+1) - Ф(λ_k) в (*) задают случайные «амплитуду» А_k = |Δ_kФ(λ)| и «фазу» θ_k = arg Δ_kФ(λ) элементарных колебаний вида

Ae^i(λt+θ) = e^iλtΔ_kФ(λ)

частоты λ, λ_k ≤ λ ≤ λ_k+1, суперпозиция к-рых в пределе дает случайный процесс Х = X(t). Переход к пределу (в среднем квадратичном) в представлении (*) осуществляется при все более мелком разбиении прямой -∞ < λ < ∞ на интервалы Δ_k = (λ_k, λ_k+1), когда max_k(λ_k+1 - λ_k) → 0. Обычно предполагают, что

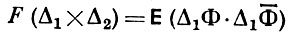
как функция множеств Δ₁ × Δ₂ на плоскости задает комплексную меру ограниченной вариации; в этом случае соответствующий процесс Ф(λ), -∞ < λ < ∞ [или точнее, соответствующая случайная мера dФ(λ)] однозначно определяется самим процессом X(t), -∞ < t < ∞:

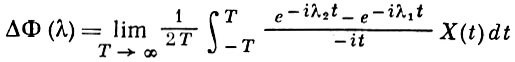
для любого интервала Δ = (λ₁, λ₂) такого, что dФ(λ₁) = dФ(λ₂) = 0 и

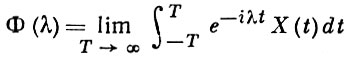
для любой точки λ, -∞ < λ < ∞. Случайный процесс X(t), -∞ < t < ∞, является Г. с. п. тогда и только тогда, когда его корреляционная функция представима в виде

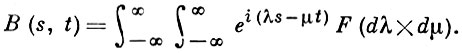
Примеры Г. с. п. 1) Стационарный случайный процесс. Если

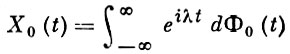
- стационарный случайный процесс, то процесс вида

X(t) = c(t) X₀(t),

где

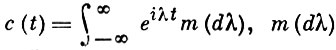
- некоторая мера на прямой, вообще говоря, уже не будет стационарным, но он будет гармонизуемым:

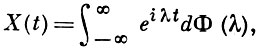
где случайная мера dФ(λ) определена формулой

ΔФ(λ) = ∫_Δ m(Δ - λ) dФ₀(λ).

2) Процесс, определяемый с помощью скользящего суммирования

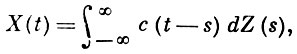
где dZ(t) - нек-рая случайная мера на прямой, а весовая функция c(t) того же типа, что и выше:

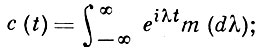
в этом случае

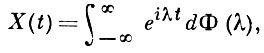
где

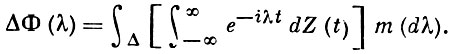
Лит.: [1] Лоэв М., Теория вероятностей, пер. с англ., М., 1962, с. 486-511.

Ю. А. Розанов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.