ГАММЕРШТЕЙНА УРАВНЕНИЕ

ГАММЕРШТЕЙНА УРАВНЕНИЕ - нелинейное интегральное уравнение вида

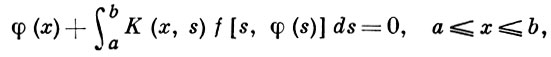
где K(x, s) и f(x, s) - заданные функции, а φ(х) -искомая функция. Названо по имени А. Гаммерштейна [1], рассмотревшего случай, когда К(х, s) есть фредгольмово симметричное и положительное ядро, т. е. все его собственные значения положительны. Если, кроме того, функция f(x, s) непрерывна и удовлетворяет условию

|f(x, s)| ≤ C₁|s| + C₂,

где С₁ и С₂ - положительные постоянные, причем С₁ меньше первого собственного значения ядра К(х, s), то Г. у. имеет по крайней мере одно непрерывное решение. Если же для любого фиксированного х из интервала (а, b) функция f(x, s) является неубывающей функцией от s, то Г. у. может иметь не более одного решения. Это последнее свойство сохраняется и в том случае, если функция f(x, s) удовлетворяет условию

|f(x, s₁) - f(x, s₂)| ≤ C|s₁ - s₂|,

где положительная постоянная С меньше первого собственного значения ядра К(х, s). Для построения решения Г. у. можно применять последовательных приближений метод.

Лит.: [1] Hammerstein A., «Acta math.», 1930, Bd 30, S. 117-76; [2] Tpикоми Ф., Интегральные уравнения, пер. с англ., М., 1960; [3] Вайнберг М. М., Вариационные методы исследования нелинейных операторов, М., 1956; [4] Красносельский М. А., Топологические методы в теории нелинейных интегральных уравнений, М., 1956; [5] Смирнов Н. С., Введение в теорию нелинейных интегральных уравнений, М.-Л., 1936.

Б. В. Хведелидзе.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.