ГАММА-ФУНКЦИЯ

ГАММА-ФУНКЦИЯ, Г-функция,- трансцендентная функция T(z), распространяющая значения факториала z! на случай любого комплексного z ≠ 0, -1, -2, .... Г.-ф. введена Л. Эйлером [(L. Euler), 1729, письмо к X. Гольдбаху (Ch. Goldbach)] при помощи бесконечного произведения

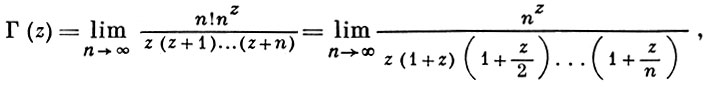
из к-рого Л. Эйлер получил интегральное представление (эйлеров интеграл второго рода)

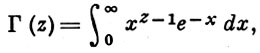
верное для Re z > 0. Многозначность функции x^z-1 устраняется формулой x^z-1 = e^{(z-1)ln x} с действительным ln х. Обозначение Г(z) и назв. Г.-ф. были предложены А. М. Лежандром (А. М. Legendre, 1814).

Если Re z < 0 и -k-1 < Re z < -k, k = 0, 1, 2, ..., то Г.-ф. может быть представлена интегралом Коши-Зальшюца:

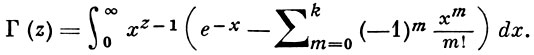
На всей плоскости z с выброшенными точками z = 0, -1, -2, ... для Г.-ф. справедливо интегральное представление Ганкеля:

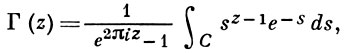
где s^z-1 = e^{(z-1)ln s}, причем ln s есть ветвь логарифма, для к-рой 0 < arg ln s ≤ 2π; контур С изображен на рис. 1. Из представления Ганкеля видно, что Г(z) -мероморфная функция. В точках z_n = -n, n = 0, 1, 2, ..., она имеет простые полюсы с вычетами (-1)ⁿ/n!

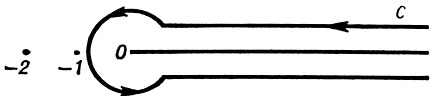
Рис. 1.

Основные соотношения и свойства Г.-ф.

1) Функциональное уравнение Эйлера:

zГ(z) = Г(z + 1),

или

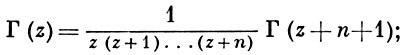
Г(1) = 1, Г(n + 1) = n!, если n > 0 - целое, при этом считают 0! = Г(1) = 1.

2) Формула дополнения Эйлера:

Г(z)Г(1 - z) = π/sin πz.

В частности,

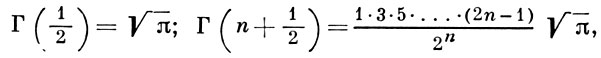
если n > 0 - целое, то

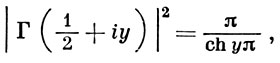
y - действительное.

3) Формула умножения Гаусса:

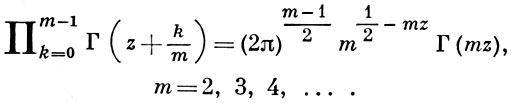
При m = 2 это есть формула удвоения Лежандра.

4) При Rе z ≥ δ > 0 или |Im z| ≥ δ > 0 имеет место асимптотич. разложение ln Г(z) в ряд Стирлинга:

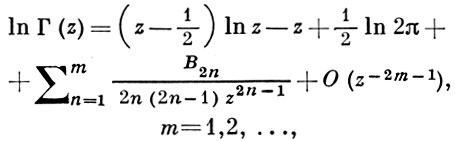
где B_2n - Бернулли числа. Из чего следует равенство

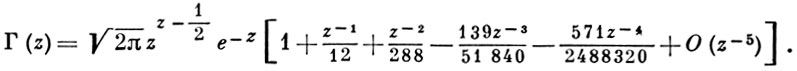
В частности,

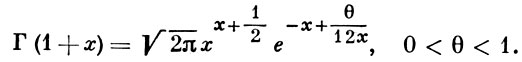
Более точной является формула Сонина [6]:

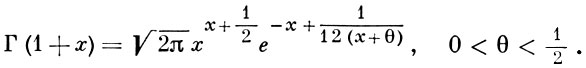
5) В действительной области Г(х) > 0 для х > 0 и принимает знак (-1)^k+1 на участках -k - 1 < х < -k, k = 0, 1, 2, ... (см. рис. 2). Для всех действительных x справедливо неравенство

ГГ'' > Г'² ≥ 0,

т. е. все ветви как |Г(x)|, так и ln |Г(х)| - выпуклые функции. Свойство логарифмич. выпуклости определяет Г.-ф. среди всех решений функционального уравнения

Г(1 + х) = хГ(х)

с точностью до постоянного множителя.

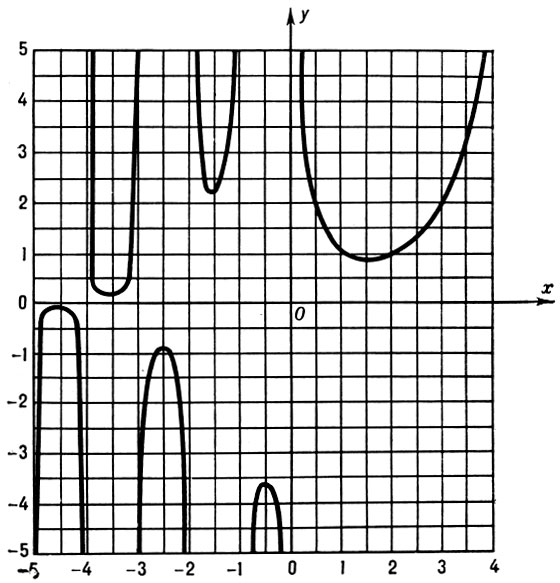
Рис. 2. График функции y = Г(х).

Для положительных х Г.-ф. имеет единственный минимум при х = 1,4616321..., равный 0,885603... . Локальные минимумы функции |Г(х)| при х → -∞ образуют последовательность, стремящуюся к нулю.

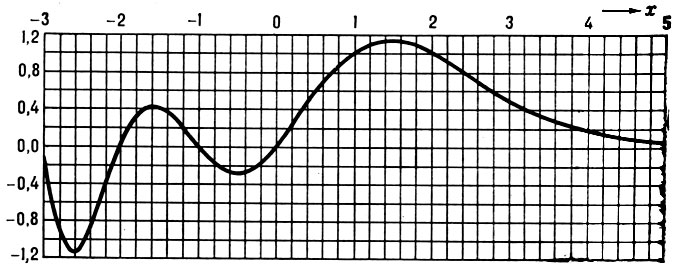
Рис. 3. График функции 1/Г(x).

6) В комплексной области, при Re z > 0, Г.-ф. быстро убывает при |Im z| → -∞

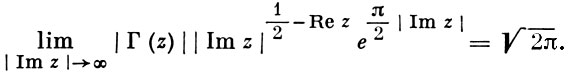
7) Функция 1/Г(z) (см. рис. 3) является целой функцией 1-го порядка максимального типа, причем асимптотически при Г → ∞

ln М(r) ~ r ln r,

где

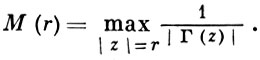
Она представима бесконечным произведением Вейерштрасса:

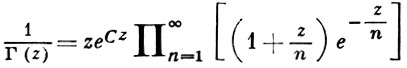
абсолютно и равномерно сходящимся на любом компактном множестве комплексной плоскости (здесь С -Эйлера постоянная). Справедливо интегральное представление Ганкеля:

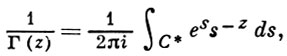
где контур С^* изображен на рис. 4.

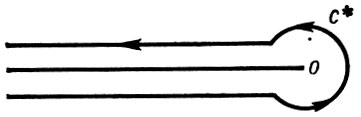
Рис. 4.

Интегральные представления для степеней Г.-ф. были получены Г. Ф. Вороным [7].

В приложениях большую роль играют так наз. полигамма-функции, являющиеся к-ми производными от ln Г(z). Функция (ψ-функция Гаусса)

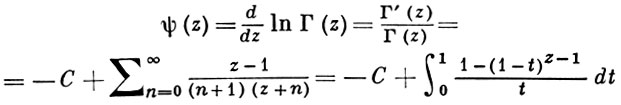
мероморфна, имеет простые полюсы в точках z = 0,- 1,_-2, ... и удовлетворяет функциональному уравнению

ψ(z + 1) - ψ(z) = 1/z.

Из представления ψ(z) при |z| < 1 следует формула

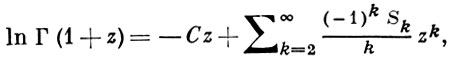
где

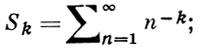
эта формула полезна для вычисления Г(z) в окрестности точки z = 1.

О других полигамма-функциях см. [2]. Неполная гамма-функция определяется равенством

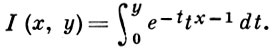
Функции Г(z), ψ(z) суть трансцендентные функции, не удовлетворяющие никакому линейному дифференциальному уравнению с рациональными коэффициентами (теорема Гёльдера).

Исключительная роль Г.-ф. в математич. анализе определяется тем, что при помощи Г.-ф. выражается большое количество определенных интегралов, бесконечных произведений и сумм рядов (см., напр., Бета-функция). Кроме того, Г.-ф. находит широкие применения в теории специальных функций (гипергеометрической функции, для которой Г.-ф. является предельным случаем, цилиндрических функций и др.), в аналитич. теории чисел и т. д.

Лит.: [1] Уиттекер Э. Т., Ватсон Дж. Н., Курс современного анализа, пер. с англ., т. 2, 2 изд., М., 1963; [2] Бейтмен Г., Эрдейи А., Высшие трансцендентные функции Гипергеометрическая функция. Функции Лежандра, пер. с англ., М., 1965; [3] Бурбаки Н., Функции действительного переменного. Элементарная теория, пер. с франц., М., 1965; [4] Математический анализ. Функции, пределы, ряды, цепные дроби, (Справочная математическая библиотека), М., 1961; [5] Nielsen N.. Handbuch der Theorie der Gamma-funktion, Lpz., 1906; [6] Сонин Н. Я., Исследования о цилиндрических функциях и специальных полиномах, М., 1954; [7] Вороной Г. Ф., Собр. соч., т. 2, К., 1952, с. 53-62; [8] Янке Е., Эмде Ф., Леш Ф., Специальные функции. Формулы, графики, таблицы, пер. с нем., 2 изд., М., 1968; [9] Анго А., Математика для электро- и радиоинженеров, пер. с франц., 2 изд., М., 1967.

Л. П. Купцов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.