ГАМИЛЬТОНОВА СИСТЕМА ЛИНЕЙНАЯ

ГАМИЛЬТОНОВА СИСТЕМА ЛИНЕЙНАЯ - система вида

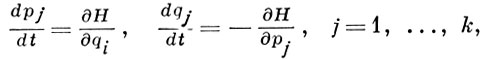
(1)

где H - квадратичная форма с действительными коэффициентами от переменных p₁, ..., p_k, q₁, ..., q_k с коэффициентами, к-рые могут зависеть от времени t. Г. с. л. наз. также линейной канонической системой. Система (1) может быть записана в векторной форме:

J dx/dt = H(t)x, (2)

где х - вектор-столбец (p₁, ..., p_k, q₁, ..., q_k), H(t) = H(t)^*- матрица квадратичной формы 2H и

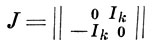
(I_k - единичная (k×k)-матрица). Уравнение (2) с произвольной неособой действительной кососимметрической матрицей J может быть сведено подходящей заменой вида x = Sx₁, где S - неособая действительная матрица, к аналогичному виду:

J₁ dx₁/dt = H₁(t)x,

здесь J₁ - любая заранее заданная действительная неособая кососимметрическая матрица. Ниже предполагается, что в (2) |Н(t)| ∈ L[t₁, t₂], ∀ -∞ < t₁ < t₂ < +∞. К канонич. уравнению (2) сводятся: векторное уравнение 2-го порядка

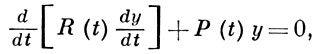
(3)

в к-ром у - вектор порядка k, R(t) = R(t)^*, Р(t) = P(t)^* - действительные (k × k)-матрицы функции, det R(t) ≠ 0; уравнение

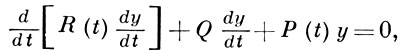
(3а)

где Q = -Q^* - постоянная матрица, R(t) = R(t)^*, P(t) = P(t)^*, det R(t) ≠ 0 (матрицы P(t), Q, R(t) -действительные), скалярное уравнение

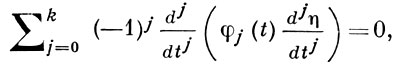
(4)

где φ_j(t) - действительные функции, φ_k(t) ≠ 0, и аналогичное векторное уравнение. [Для уравнения (3)

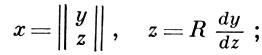
для уравнения (3а)

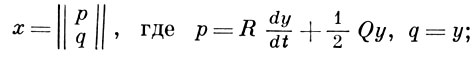
для уравнения (4) x_j = η^j-1, j = 1, ..., k,

x_j+k = φ_jx_j+1 - x'_k+j+1, j = 1, ..., k-1, x_2k = φ_kx'_k].

Скалярное уравнение (3) с R(t) = 1, т. е. уравнение d²y/dt² + P(t)y = 0, в к-ром Р(t) - периодич. функция, наз. уравнением Хилла.

Пусть X(t) - матрицант уравнения (2) [матрица фундаментальной системы решений уравнения (2), нормированная условием X(0) = I_n]. Введем индефинитное скалярное произведение 〈х, y〉 = i(Jx, у), где

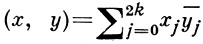
- обычное скалярное произведение. Матрица U (вообще комплексная), унитарная в смысле этого произведения, т. е. такая, что U * JU = J, наз. J-унитарной; действительная J-унитарная матрица X наз. симплектической.

Известно (см. Гамилътонова система), что при сдвиге вдоль траектории Г. с. сохраняется интегральный инвариант Пуанкаре - внешняя дифференциальная форма

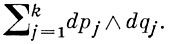
В случае Г. с. л. это свойство означает, что для любых решений x⁽¹⁾ = x⁽¹⁾(t), х⁽²⁾ = х⁽²⁾(t) уравнения (2) выполнено 〈x⁽¹⁾, х⁽²⁾〉 = 〈X(t)x⁽¹⁾ (0), X(t)x⁽²⁾(0)〉 = const, т. е. что матрицант X(t) - симплектическая матрица для любого t. Из соотношения X * JX = J следует (теорема Ляпунова-Пуанкаре), что собственные значения симплектической матрицы X (с учетом их кратностей и порядков жордановых ящиков) располагаются симметрично (в смысле инверсии) относительно единичной окружности. Собственные значения симплектических (и J-унитарных) матриц, равные по модулю 1, подразделяются на собственные значения 1-го и 2-го рода по следующему правилу. Пусть ρ - собственное значение J-унитарной матрицы U и |ρ| = 1. Тогда форма 〈х, x〉 на соответствующем корневом подпространстве не вырождается. Пусть р - число положительных и q - число отрицательных ее квадратов; говорят, что в точке ρ совпало р собственных значений 1-го рода и q собственных значений 2-го рода.

Аналогично определяется род чисто мнимых собственных значений матриц K = J^-1L, L^* = L (для них 〈Кх, у〉 = -〈х, Ку〉, ∀х, у). Для J-унитарной матрицы X собственные значения ρ при |ρ| ≠ 1 считаются собственными значениями 1-го рода, если |ρ| < 1, и 2-го рода, если |ρ| > 1. Любая симплектическая матрица X имеет (с учетом кратности) ровно k собственных значений ρ₁, ..., ρ_k 1-го рода и k значений ρ^-1₁, ..., ρ^-1_k 2-го рода. При соответствующей нумерации ρ₁, ..., ρ_k являются непрерывными функциями матрицы X(см. [2], [3]).

1. Осцилляторные свойства решений Г. с. л. К изучению осцилляторных свойств решений уравнений (2)-(4) приводит ряд задач вариационного исчисления, оптимального управления, исследование свойств спектра соответствующего дифференциального оператора и др.

Определения. (I) Уравнение (3) наз. колебательным, если для любого t₀ > 0 найдутся числа t₂ > t₁ > t₀ и решение y(t) ≢ 0 такие, что у(t₁) = y(t₂) = 0, и неколебательным - в противном случае. (II) Уравнение (4) наз. колебательным, если для любого t₀ > 0 найдется решение η(t) ≢ 0, имеющее по крайней мере два k-кратных нуля t₂ > t₁ > t₀, и неколебательным - в противном случае. (III) Уравнение (1) наз. колебательным, если на (t₀, ∞) функция

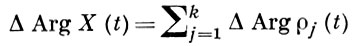
(5)

является неограниченной, и неколебательным в противном случае. [В(5) ρ_j(t) суть собственные значения 1-го рода матрицы X(t).] После сведения уравнения (3) или (4) к уравнению (2) получающееся уравнение (2) будет колебательным в смысле определения (III) тогда и только тогда, когда уравнение (3) [соответственно (4)] колебательно в смысле определения (I) [соответственно (II)]. Определению (III) можно придать следующую геометрич. интерпретацию. Группа Sp(k, R) симплектических матриц X гомеоморфна произведению связного и односвязного топологич. пространства на окружность. Соответствующее отображение можно выбрать так, что

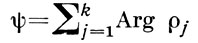
является проекцией матрицы X ∈ Sp(k, R) на окружность (числа ρ_j - собственные значения 1-го рода матрицы X). Таким образом, уравнение (2) колебательно, если при t → ∞ матрица X(t) неограниченно «закручивается» в Sp(k, R). (При n = 1 эта группа гомеоморфна «сплошному тору» и «закручивание» имеет очевидный наглядный смысл.) Известны другие разнообразные определения аргумента симплектической матрицы, соответствующие другим отображениям группы Sp(k, R) на окружность и эквивалентные (5) в том смысле, что при любом из них выполнено неравенство:

|Δ Arg'X(t) - Δ Arg X(t)| < c (6)

для любой кривой X(t) ∈ Sp (k, R). Такими аргументами являются, напр.,

Arg₁ X = Arg det(U₁ - iV₁); Arg₂ X = Arg det (U₂ - iV₂),

где U_j, V_j - сутъ (k × k)-подматрицы матрицы

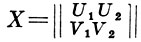
(см. также [4]). Известны разнообразные эффективно проверяемые достаточные (а в нек-рых случаях необходимые и достаточные) условия колебательности и неколебательности уравнений (2), (3), (4) (см., напр., [5] и литературу в [6]).

2. Г. с. л. с периодическими коэффициентами. Пусть в (2) Н(t + Т) = Н(t) почти всюду. Матрица X(Т) наз. матрицей монодромии уравнения (2), а ее собственные значения -мультипликаторами уравнения (2). Уравнение (2) (или соответствующий гамильтониан Н(t)) наз. сильно устойчивым, если все его решения ограничены на (-∞, +∞), и это свойство не нарушается при малых деформациях гамильтониана в смысле нормы ||H|| = ∫^T₀|Н(t)|dt. Аналогично определяется сильная неустойчивость уравнения (2) (гамильтониана H(t)). Для сильной устойчивости уравнения (2) необходимо и достаточно чтобы все его мультипликаторы лежали на единичной окружности и среди них не было совпадающих разного рода (иначе, чтобы все корневые подпространства у X(Т) были дефинитны в смысле произведения 〈х, y〉 = i(Jx, у)). Для сильной неустойчивости уравнения (2) необходимо и достаточно, чтобы нек-рые его мультипликаторы лежали вне единичной окружности. Два набора мультипликаторов (с учетом их рода), среди к-рых нет совпадающих разного рода, наз. эквивалентными, если один набор можно непрерывно перевести в другой без встречи мультипликаторов разного рода. Класс эквивалентных наборов мультипликаторов наз. мультипликаторным типом. В случае устойчивости имеется 2^k мультипликаторных типа. Их можно обозначить символами вида μ = (+, +, -, +, ..., -), в к-рых полюсы и минусы соответствуют роду мультипликаторов, последовательно встречающихся при прохождении верхней полуокружности |ρ| = 1 от точки ρ = +1 к точке ρ = -1. Пусть L = {Н(t)} -множество всех гамильтонианов указанного выше вида с нормой ||H|| = ∫^T₀|Н(t)|dt. Множество O ⊂ L сильно устойчивых гамильтонианов распадается в L на счетное число областей O^(μ)_n, n = 0, ±1, ±2, ..., μ = μ₁, ..., μ_2k. Область O^(μ)_n является множеством всех гамильтонианов, к-рым отвечают мультипликаторный тип μ и целое число n, определяемое формулой

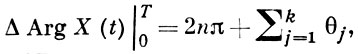
где θ_j = arg ρ_j(Т) - аргументы мультипликаторов 1-го рода (см. [4], [7]). Для k = 1 множество сильно неустойчивых гамильтонианов распадается на счетное число областей; при k > 1 это множество связно. Известны (см. [3], [7], [8]) разнообразные достаточные условия принадлежности Н(t) ∈ O^(μ)_n. При получении этих условий важную роль играет следующая теорема: пусть H₁(t) ≤ H₂(t), тогда из сильной устойчивости «отрезка» H_s(t) = sH₁(t) + (1 - s) H₂(t), 0 ≤ s ≤ 1, следует сильная устойчивость любого гамильтониана Н(t) такого, что H₁(t) ≤ H(t) ≤ H₂(t). Аналогичная теорема установлена и для бесконечномерного случая (k = ∞), когда {х} - гильбертово пространство и в (2) J, Н(t) суть операторы со специальными свойствами (см. [9]); при k = 1 эта теорема верна и для сильно неустойчивых гамильтонианов [3].

3. Параметрический резонанс.

Рассмотрим уравнение

J dx/dt = H₀x (8)

с постоянным гамильтонианом Н₀ таким, что все решения уравнения (8) ограничены. Частота θ наз. критической, если для любого δ > 1 найдется «возмущенное» гамильтоново уравнение

J dx/dtJ =H#θt*x*, (9)

где H(t + 2π) = H(t), ||H(t) - H₀|| < δ, такое, что уравнение (9) имеет неограниченные решения (знак у θ может быть любым). Явление возникновения неограниченно нарастающих колебаний системы при сколь угодно малом периодическом возмущении нек-рых ее параметров наз. параметрическим резонансом. Параметрич. резонанс имеет большое значение в технике и физике. Он «опаснее» (или «полезнее», в зависимости от задачи) обычного резонанса, поскольку в отличие от последнего при нем колебания нарастают по экспоненциальному закону (а не степенному), и частоты, при к-рых имеет место резонанс, заполняют малые интервалы. Длины этих интервалов зависят от амплитуды возбуждения, а сами интервалы стягиваются в точки (соответствующие критич. частотам), когда амплитуда возбуждения стремится к нулю. Пусть iω₁, ..., iω_k - собственные значения 1-го рода матрицы J^-1H₀ (тогда -iω₁, ..., -iω_k имеют 2-й род). Пусть ω_j + ω_h ≠ 0 (j, h = 1, ..., k). Критич. частотами являются числа θ^(N)_jh = (ω_j + ω_h)/N (j, h = 1, ..., k, N = ±1, ±2, ...) и только они (см. [2]). Пусть в (9) Н(θt) = Н₀ + εН₁ (θt), ε - малый параметр;

J^-1H₀f_j = iω_if_j (j = ±1, ±2, ..., ±k), w_j = -ω_j, H₁(τ) = ∑_m H^(m)e^imτ.

Систему векторов f_j можно выбрать нормированной условием 〈f_j, f_h〉 = δ_jh sign j (j = ±1, ..., ±k). На плоскости {ε, θ} вблизи оси θ точки {ε, θ}, для к-рых уравнение (9) с Н(θt) = H₀ + εH₁ (θt) сильно неустойчиво, заполняют области Ω₁(ε) < θ - θ^(N)_jh < Ω₂(ε), примыкающие к точкам (0, θ^(N)_jh), где Ω_1,2 = θ^(N)_jh + εμ_1,2 + O(ε^3/2) (имеется в виду «общий» случай, см. [3]). Числа μ₁, μ₂ просто выражаются через Н^(m) и f_j (см., напр., [3]).

Величина |(H^(N)f_j, f_-h)| характеризует «степень опасности» критич. частоты θ^(N)_jh: чем больше эта величина, тем шире «клинышек» неустойчивости, примыкающий к точке (0, θ^(N)_jh), и тем ближе к оси θ подходит внутри этого клинышка область α - экспоненциального возрастания решения с малым α > 0 (подробнее см. в [3]). Другие сведения имеются в [10], [12], [13].

Результаты, аналогичные перечисленным, имеются для уравнений (1) с комплексными коэффициентами (Н(t) - эрмитова матрица функции, J^* = -J, det J ≠ 0, см., напр., [11]). В работе [14] рассмотрена более общая система

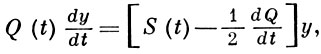
где

Q(t)^* = -Q(t), S(t)^* = S(t), det Q(t) ≠ 0, Q(t + T) = Q(t), S(t + T) = S(t).

Выяснено, что как в комплексном, так и в действительном случаях имеется конечное число областей устойчивости, получены их характеристики в терминах свойств решений соответствующих уравнений.

Ряд аналогичных результатов получен также для операторных уравнений (2) в гильбертовом пространстве с ограниченными и неограниченными операторными коэффициентами (см. [15], [16]).

Лит.: [1] Ляпунов А. М., Общая задача об устойчивости движения, Собр. соч., т. 2, 1956, с. 7-263; [2] Крейн М. Г., в сб.: Памяти А. А. Андронова, М., 1955, с. 413-98; [3] Якубович В. А., Старжинский В. М., Линейные дифференциальные уравнения с периодическими коэффициентами и их приложения, М., 1972, гл. 3; [4] Гельфанд И. М., Лидский В. В., «Успехи матем. наук», 1955, т. 10, № 1, с. 3-40; [5] Sternberg R. L., «Duke Math. J.», 1952, v. 19, № 2, p. 311-22; [6] Якубович В. А., «Матем. сб.», 1962, т. 56 (98), № 1, с. 3-42; [7] Крейн М. Г., Якубович В. А., в кн.: Тр. Международного симпозиума по нелинейным колебаниям, т. 1, К., 1963, с. 277-305; [8] Лидский В. В., «Докл. АН СССР». 1955, т. 102, № 5, с. 877-80; [9] Дергузов В. М., «Матем. сб.», 1964, т. 63 (105), № 4, с. 591-619; [10] Моsеr J., «Comm. Pure Appl. Math.», 1958, v. 11, № 1, p. 81-114; [11] Соppel W. A., Howe A., «J. Austral. Math. Soc.», 1965, v. 5, № 2, p. 169-95; [12] Митропольский Ю. А., Метод усреднения в нелинейной механике, К., 1971; [13] Еругин Н. П., Линейные системы обыкновенных дифференциальных уравнений с периодическими и квазипериодическими коэффициентами, Минск, 1963; [14] Лидский В. В., Фролов П. А., «Матем. сб.», 1966, т. 71 (113), № 1, с. 48-64; [15] Далецкий Ю.Л., Крейн М. Г., Устойчивость решений дифференциальных уравнений в банаховом пространстве, М., 1970, гл. 5; [16] Фомин В. Н., Математическая теория параметрического резонанса в линейных распределенных системах, Л., 1972.

В. А. Якубович.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.