ГАМИЛЬТОНА-ЯКОБИ ТЕОРИЯ

ГАМИЛЬТОНА-ЯКОБИ ТЕОРИЯ - раздел классического вариационного исчисления и аналитич. механики, в к-ром задача нахождения экстремалей (или задача интегрирования гамильтоновой системы уравнений) сводится к интегрированию нек-рого уравнения с частными производными 1-го порядка - так наз. уравнения Гамильтона-Якоби. Основы Г.-Я. т. были разработаны У. Гамильтоном (W. Hamilton) в 20-х гг. 19 в. в применении к задачам волновой и геометрич. оптики. В 1834 У. Гамильтон распространил свои идеи на задачи динамики, а в 1837 К. Якоби (С. Jacobi) применил этот метод для общих задач классического вариационного исчисления.

Исходные позиции Г.-Я. т. были заложены в 17 в. П. Ферма и X. Гюйгенсом на материале геометрия, оптики (см. Ферма принцип и Гюйгенса принцип). Рассмотрим, следуя У. Гамильтону, задачу о распространении света в неоднородной (но для простоты - изотропной) среде, где v(х)- локальная скорость света в точке х. В соответствии с принципом Ферма свет в неоднородной среде распространяется от точки к точке за кратчайшее время. Пусть х₀ ∈ Е исходная тонка, а W(x) - минимальное время, требуемое свету для преодоления пути от x₀ к х. Функцию W (х) называют эйконалом, или оптической длиной пути. Допустим, что за малое время dt свет распространился из точки х до точки x + dx. В соответствии с Гюйгенса принципом свет с точностью до малых более высокого порядка будет распространяться по нормали к поверхности уровня функции W(x). Таким образом выполняется равенство

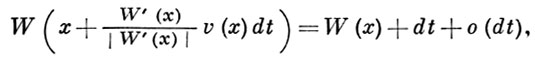
из к-рого следует уравнение Гамильтона-Якоби для задач геометрич. оптики:

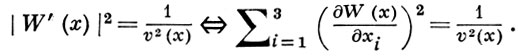
В аналитич. механике роль принципа Ферма играет вариационный Гамильтона-Остроградского принцип, а роль эйконала играет функция действия, представляющая собой интеграл

S(t, x) = ∫_ν L dt, x = (x₁, ..., x_n), (1)

вдоль траектории ν, соединяющей фиксированную точку (t₀, х₀) с точкой (t, х), где L - функция Лагранжа механич. системы.

К. Якоби предложил рассматривать функцию действия, подобную (1), для любой задачи классического вариационного исчисления. Экстремали задачи ∫ Ldt → inf, исходящие из точки (t₀, х₀), пересекают поверхность уровня функции действия трансверсально (см. Трансверсальности условие), из этого выводят вид дифференциала функции действия:

dS = (p | dx) - Hdt,

где p = L_ẋ, а Н = рẋ - L - Гамильтона функция (см. также Лежандра преобразование).

Последнее соотношение приводит к уравнению для функции S:

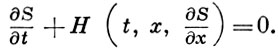
Это уравнение и наз. уравнением Гамильтона-Якоби.

Важнейшим результатом Г.-Я. т. является теорема Якоби, заключающаяся в том, что полный интеграл уравнения (2), т. е. решение S(t, х, α) этого уравнения, зависящее от параметров α = (α₁, ..., α_n) (с условием невырожденности 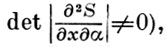позволяет получить общий интеграл уравнения Эйлера функционала (1), или, что то же самое, - гамильтоновой системы, связанной с этим функционалом, по формулам

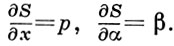
Применение теоремы Якоби к интегрированию гамильтоновых систем основано, как правило, на методе разделения переменных в специально выбранных координатах.

Несмотря на то, что интегрирование уравнении с частными производными составляет, как правило, более сложную задачу, чем отыскание решений обыкновенных уравнений, Г.-Я. т. оказалась мощным орудием исследования задач оптики, механики и геометрии. Суть принципа Гюйгенса была применена Р. Беллманом (R. Bellmann) к задачам оптимального управления.

См. также Гильберта инвариантный интеграл.

Лит.: [1] Вариационные принципы механики, М., 1959; [2] Парс Л.-А., Аналитическая динамика, пер. с англ., М., 1971, с. 283-86; [3] Арнольд В. И., Математические методы классической механики, М., 1974, с. 219-24; [4] Ахиезер Н. И., Лекции по вариационному исчислению, М., 1955, с. 92-96.

В. М. Тихомиров.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.