ГАМИЛЬТОНА ФУНКЦИЯ

ГАМИЛЬТОНА ФУНКЦИЯ, гамильтониан,- функция, введенная У. Гамильтоном (W. Hamilton, 1834) для описания движений механических систем; начиная с работ К. Якоби (К. Jacobi, 1837), используется в классическом вариационном исчислении для представления Эйлера уравнений в канонической форме. Пусть L(t, х, ẋ) - Лагранжа функция механич. системы или подинтегральная функция в задаче минимизации функционала

J(х) = ∫ L (t, хẋ) dt

классического вариационного исчисления, где х = (х₁, ..., х_n), det||L_x∏|| ≠ 0. Г. ф. представляет собой Лежандра преобразование функции L по переменным ẋ, иначе говоря,

H(t, х, р) = (р| ẋ) - L(t, х, ẋ),

где ẋ выражено через р соотношением р = L_ẋ; (р| ẋ) - скалярное произведение векторов р = (p₁, ..., p_n) и ẋ. С помощью Г. ф. уравнения Эйлера

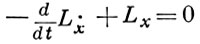
(в задачах классич. механики называемые Лагранжа уравнениями) записываются в виде системы уравнений 1-го порядка:

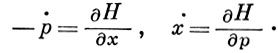
Эти уравнения наз. Гамильтона уравнениями, гамильтоновой системой, а также канонической системой. Через Г. ф. пишутся уравнения Гамильтона-Якоби для функции действия (см. Гамильтона-Якоби теория).

Г. ф. в задаче оптимального управления определяется следующим образом. Пусть требуется найти минимум функционала

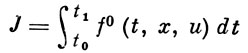
при дифференциальных связях

ẋⁱ = fⁱ(t, х, u),

при заданных граничных условиях и ограничении на управление u ∈ U. Здесь х = (x₁, ..., x_n) есть n-мерный вектор фазовых координат, u = (u', ..., u^m) - m-мерный вектор управления, U - замкнутое множество допустимых значений управления u. Г.ф. в этой задаче имеет вид

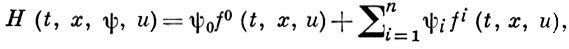
где ψ₀ = соnst ≤ 0, ψ₁, ..., ψ_n - сопряженные переменные (множители Лагранжа, импульсы), аналогичные введенным выше канонич. переменным р_i. Если (х₀, u₀) есть минимум в поставленной задаче и ψ₀ ≠ 0 (тогда ψ₀ можно считать равным -1), то

H(t, x₀(t), p(t), u₀(t)) = (p|f)|_x0,u0 - f⁰|_x0u0,

где

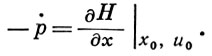
Полученное для Г. ф. выражение имеет ту же структуру, что и в классическом вариационном исчислении. Согласно Понтрягина принципу максимума уравнения Эйлера для задачи оптимального управления с помощью Г. ф. можно записать в виде

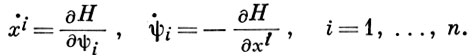
Оптимальное управление и при каждом t должно доставлять максимум Г. ф.:

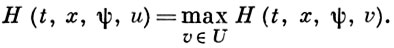
Лит.: [1] Блисс Г. А., Лекции по вариационному исчислению, пер. с англ., М., 1950; [2] Понтрягин Л. С., [и др.], Математическая теория оптимальных процессов, 2 изд., М., 1969.

И. Б. Вапнярский.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.