ГАМИЛЬТОНА УРАВНЕНИЯ

ГАМИЛЬТОНА УРАВНЕНИЯ - канонические обыкновенные дифференциальные уравнения 1-го порядка, описывающие движения голономных механич. систем под действием приложенных к ним сил, а также экстремали задач классического вариационного исчисления.

Г. у., установленные У. Гамильтоном [1], эквивалентны Лагранжа уравнениям 2-го рода (или Эйлера уравнениям в классическом вариационном исчислении), в к-рых неизвестными являются обобщенные координаты q_i, а также и q̇_i = dq_i/dt. Вместо обобщенных скоростей q̇_i У. Гамильтон ввел в рассмотрение обобщенные импульсы

p_i = ∂L/∂q̇i, i = 1, ..., n, (1)

где L(q_i, q̇_i, t) - Лагранжа функция, n - число степеней свободы системы, и определил функцию

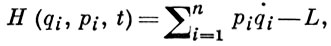
(2)

наз. ныне Гамильтона функцией. В правой части (2) переменные q̇_i заменяются их выражениями

q̇_i = φ_i(q_s, p_s, t)

получаемыми разрешением уравнений (1). Для динамич. систем, у к-рых

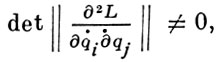
такое разрешение всегда возможно.

Г. у. имеют вид канонич. уравнений

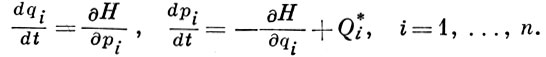
Здесь Q^*_i обозначают непотенциальные обобщенные силы, если они действуют на систему. Число уравнений (3) равно числу 2n неизвестных q_i, р_i.

Порядок системы (3) как и системы уравнений Лагранжа 2-го рода, равен 2n.

Переход от переменных q_i, q̇_i, t и функции Лагранжа L к переменным q_i, р_i, t и функции Гамильтона H, согласно формулам (1) и (2), представляет собой Лежандра преобразование. Г. у. имеют определенные преимущества по сравнению с уравнениями Лагранжа, что обусловило их большую роль в аналитич. механике. См. также Гамильтонова система.

Лит.: [1] Hamilton W. R., «Philos. Trans. Roy. Soc. London», 1835, pt 1, p. 95-144.

В. В. Румянцев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.